Problem
If you don’t know anything about electricity, read the next bit to learn all you need to know to solve the following problem. The voltage, V, between the ends of a resistor, R, is related to the current I, flowing through the resistor by Ohm’s Law, V = IR (volts = amperes x ohms). Voltages in series add up, and whatever current flows into a point must flow out. A good ammeter has essentially zero resistance.
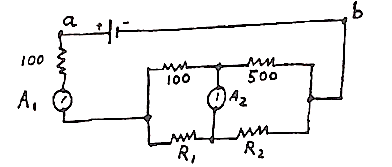
A battery maintains two volts between points a and b. The value of the resistors (WW) are shown in ohms. Ammeter A, reads 8 milliamperes and ammeter A2 reads zero. What is the value of R1 in ohms?
(a) 33.3
(b) 50
(c) 66.7
(d) 166.7
(e) 300
Solution
(a) 33.3
Once again, an electrical problem rears its ugly head and only one third answer it, with one third of them correct. All you need to know was given to you. Since 8ma flows through the left hand 100 Ω resistor, it drops .008 x 100 = 0.8 volts. This leaves 2 – 0.8 = 1.2 volts drop across the rest of the circuit. Ohm’s Law again tells us that 1.2/600 = 0.002 amps flow via the top branch (100 + 500) Ω, leaving the rest, 0.008 – 0.002 = 0.006 amps, to flow through the bottom branch (R1 + R2). Since no current flows via A2, the voltage drop across the 100 Ω in the top branch must equal the voltage drop across R1 in the bottom. But we now know the current in each resistor.
∴ (0.002)(100) = (0.006) R1, R1 = 33.3 Ω
Some students with electronics experience might recognize this as a balanced Wheatstone bridge, but that wouldn’t help them too much.