Disordered Magnetic Materials
Systems of interacting magnetic moments have long been used by physicists as a basis for studying and testing numerous models in statistical physics. Magnetic systems may often possess a well-defined Hamiltonian to use as a starting point for understanding the nonetheless very complex behaviour that may result. One of the most difficult of such models to study theoretically is the effect of disorder which may be caused by random interactions between spins or by a random dilution of the magnetic ions with non-magnetic species. In some instances, such disordered systems exhibit what is known as a "spin glass" phase. As the temperature of the system is lowered, the spin dynamics get progressively slower until one reaches a transition temperature where the spins are completely frozen in place, but still randomly oriented. This frozen disorder is analogous to the frozen structural disorder seen in real glasses, hence the name. Spin glass models can also be related to models of such diverse systems as neural networks, biological evolution and the internet!
We are studying the set of materials LiHoxY1-xF4 where x is the concentration of magnetic holmium ions which have been diluted by non-magnetic yttrium ions. At high concentrations of holmium, this material is a ferromagnet, but at x = 0.25, it begins to show glassy behaviour. The holmium moments are nearly perfect Ising moments and interact primarily via dipolar interactions, thus the Hamiltonian or underlying model of this system is seemingly well understood. Nonetheless, both theoretical simulations and experiments on this system have come to differing views on whether it truly undergoes a spin glass transition or not. The existence of an unfrozen spin liquid or "antiglass" state was also proposed by other researchers to exist at x = 0.045.
Our measurements of the specific heat of several of these materials have discounted the existence of much of the exotic "antiglass" physics that was published previously. What was seen, however, is the existence of an increasing residual entropy with lower concentration. This is reminiscent of some Monte Carlo results showing the materials to not undergo a finite temperature spin glass transition. Currently, we are probing this system with a SQUID (Superconducting QUantum Interference Device) magnetometer which is able to measure the extremely slow dynamics seen in these glassy systems.
Geometric frustration
Geometric frustration arises in magnetic materials when there is no ground state which allows all the pairs of interactions to be satisfied simultaneously. This is most easily illustrated with spins occupying the corners of a triangle interacting with each other antiferromagnetically (preferring to be oppositely aligned). two of the spins may point in opposite directions from each other, thereby satisfying the antiferromagnetic interaction, but the third is then frustrated, unable to choose an ideal configuration. Geometric frustration can lead to a variety of very interesting magnetic properties. Often, a material's magnetic ordering temperature is greatly reduced or even completely suppressed by the frustration. Spin glasses (frozen disorder), spin liquids (dynamic spins) and spin ice (a magnetic analog of water-ice) are some of the more unusual states resulting from geometric frustration.
We are studying several geometrically frustrated materials. Examples include materials based on the pyrochlore lattice, a network of corner-sharing tetrahedra. In particular, we have studied the specific heat of Gd2Sn2O7 (GSO), a realization of a Heisenberg (large-S) magnet on a pyrochlore lattice. GSO is found to order at around 1 K into a staggered, antiferromagnetic ground state. However, measurements which are able to probe the dynamics of the spins such as μSR and Mossbauer spectroscopy suggest that the spins remain unfrozen down to very low temperatures, exhibiting persistent spin dynamics (PSDs). These dynamics are found in many pyrochlore magnets and are poorly understood. Our measurements of the specific heat, along with calculations by Adrian del Maestro and Michel Gingras, have demonstrated that the material shows a conventional ordered state with a gapped spin-wave spectrum implying that the spins must be largely freezing in place at lower temperatures instead of remaining dynamic as is suggested by other measurement techniques.

Heat capacity cell
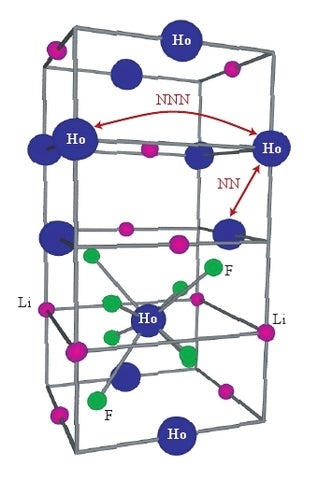
Crystal structure
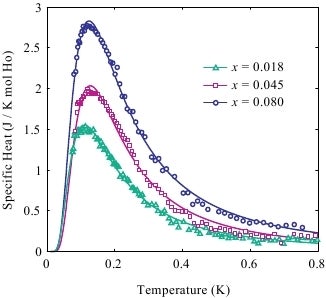
Sample specific heat data for LiHoxY1-xF4

A pyrochlore lattice with monopoles and stuffed spins