
Hyperbolic Lattice Simulations
Motivated by recent developments in hyperbolic band theory, hyperbolic metamaterials, and hyperbolic error correction codes, we expolre a novel way of realizing hyperbolic phenomena in the Poincaré disk model directly on a superconducting device.
Our approach leverages high-Q resonators to resolve the fine details in the spectroscopy. Meanwhile, it mimics the non-uniform hyperbolic distance in the curved space electromagnetically by imposing variations in the capacitive couplings between resonators. We use this approach to experimentally realize a sublattice of the octagonal tiling of the Bolza surface. We also demonstrate, for the first time, an experimental realization of a hyperbolic lattice in a higher-genus Riemann surface (g=3). The experimental results are compared to numerical solutions predicted by hyperbolic band theory and the classical circuit simulations.
Our approach furthers the study and simulation of physics in negatively curved spaces through synthetic means.
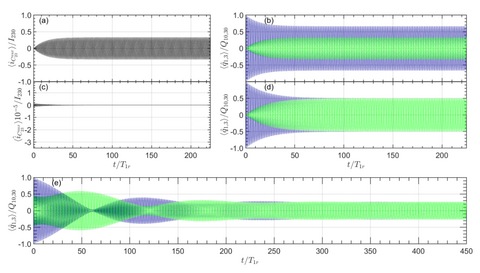
Achieving perfect synchronization of quantized charges with asynchronous initial dynamics.
Quantum Synchronization
In neuromorphic computing, neural networks often rely on collective phenomena, such as the synchronization of dynamics between neurons, to execute various computational tasks. However, in the quantum regime, the impact noise and dissipation have in influencing the necessary collective effects required for quantum neuromorphic computing (QNC) is still not fully understood. This is particularly true for the theoretical and experimental development of quantum synchronization in superconducting circuits, which is a leading architecture to implement QNC.
In our theoretical work we have shown that a passive resistive circuit element is sufficient to robustly produce quantum synchronization in devices that are mutually coupled to this lossy environment. This was done using the novel approach of a Rayleigh dissipation function compared to standard Lindblad method of open quantum systems.
The continuation of this project includes experimentally realizing quantum synchronization using superconducting circuits and extending the theoretical investigation to other collective quantum properties, such an entanglement.