Loading Conditions and Paths
Proportional Loading
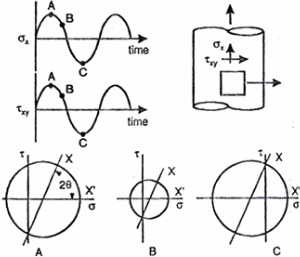
Nonproportional loading
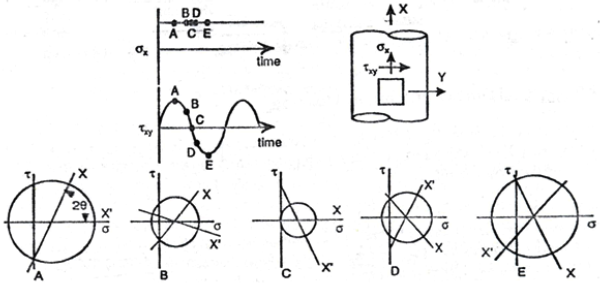
Various nonproportional loading paths
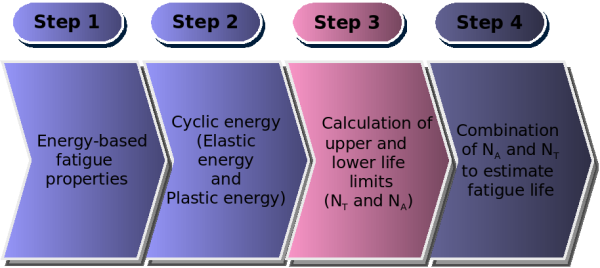
Proposed Fatigue Life Model
Total strain-life equation (Δε-N or Coffin-Manson)
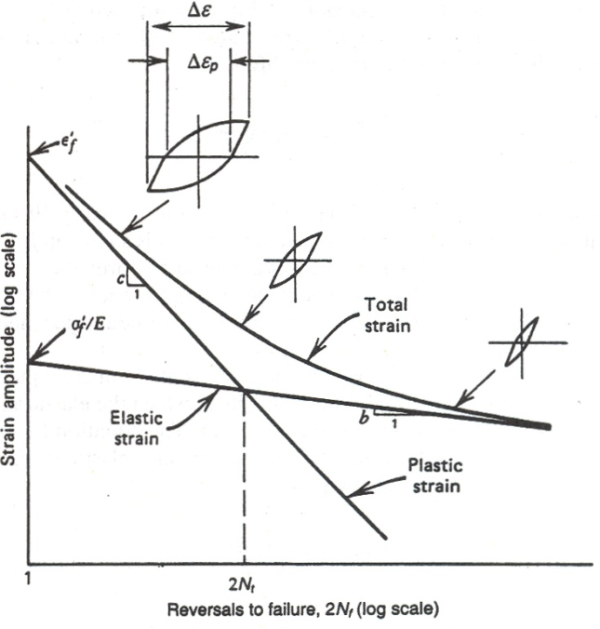
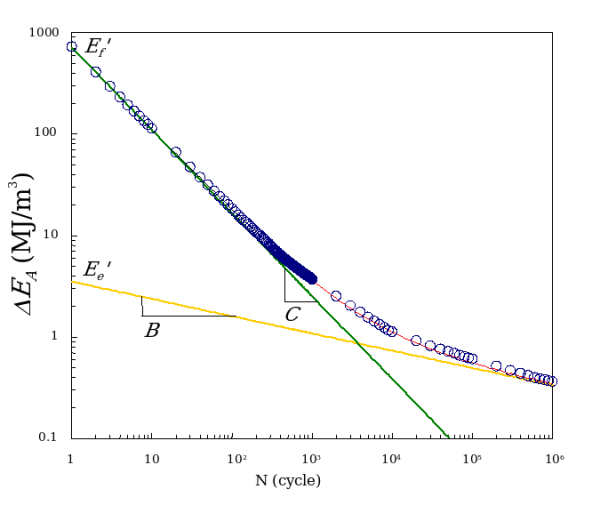
Energy-life equation (ΔE-N)
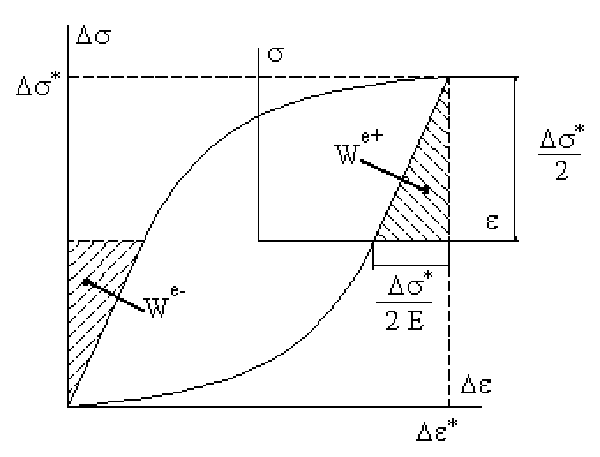
-
Cyclic
energy
calculation
-
Tension,
Torsion
or
Proportional
loading
- Variable Material Property (VMP) method (Jahed et al. (1997) )
-
Tension,
Torsion
or
Proportional
loading
-
Nonproportional
loading
- An incremental cyclic plasticity model
For more information see: Autofretaged and Pressurized tubes (Jahed, 1997), Rotating disks (Jahed, 2000), Unloading behaviour of a thermoplastic disk (Jahed, 2001).
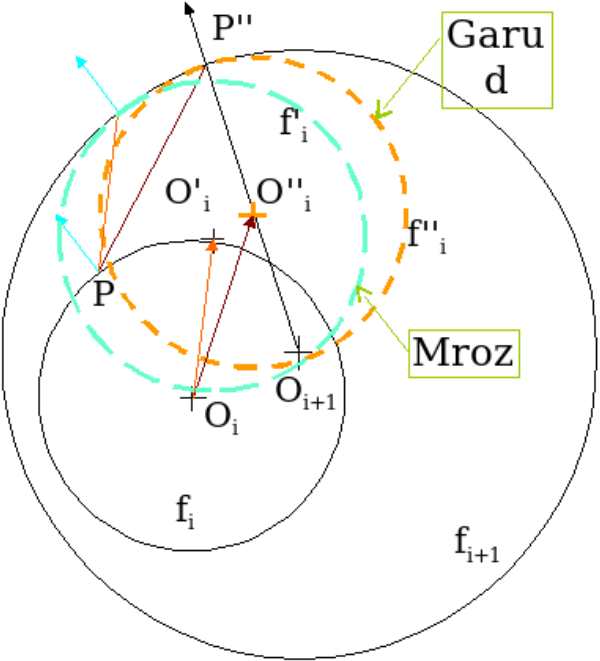
Cyclic Plasticity Models
- Yield function: von Mises
- Flow rule: normality condition
- Hardening rule: kinematic hardening rule of Mroz and Garud
Comparative representation of Mroz's and Garud's cyclic plasticity models:
Application of The Proposed Life Model to Nonproportional Loading
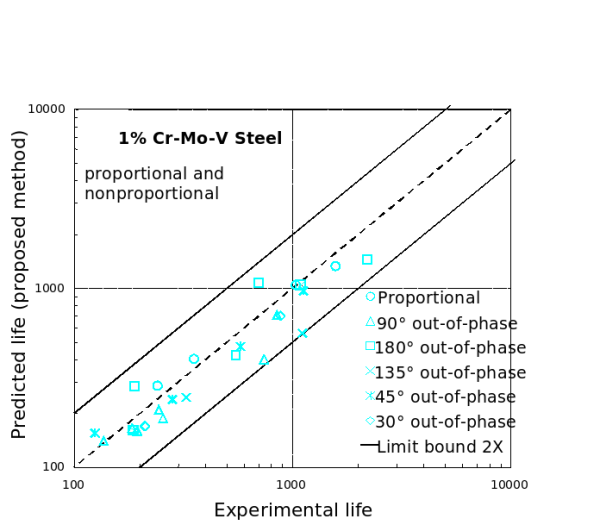
- 1% Cr-Mo-V Steel
Loading: Out of Phase φ=135° εa=1.01 Υa=1.52
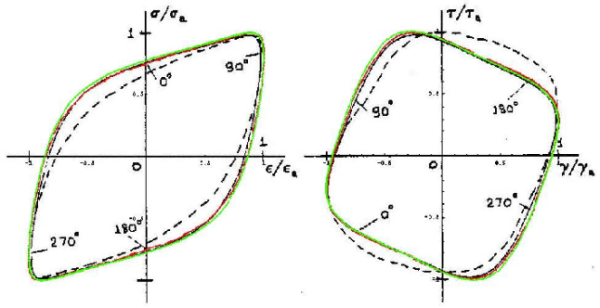
Verification of plastic energy calculation of the cyclic plasticity model
- 1% Cr-Mo-V Steel
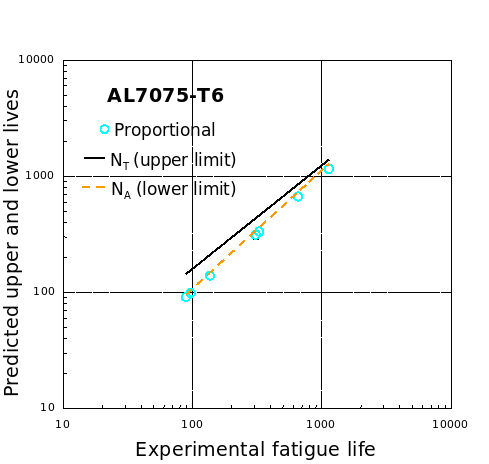
- 7075-T6 Al
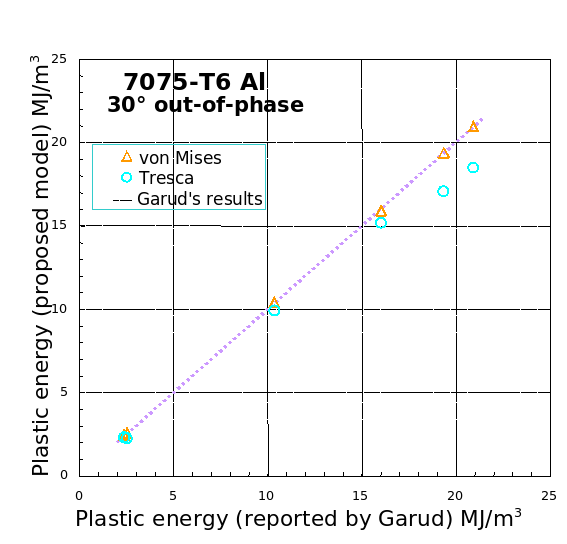
Energy-life
curves
and
corresponding
energy-based
fatigue
properties
Curve
fitting
of
energy-life
data
points
- Logarithmic fitting (E=a Log(N) + b)
- Direct fitting (E=C Nd )
| B | C | Bs | Cs | E'e | E'f | W'e | W'f | |
|---|---|---|---|---|---|---|---|---|
| 1% CrMoV | -0.112 | -0.765 | -0.1034 | -0.782 | 3.658 | 1139.3 | 3.3712 | 2674.78 |
| Al7075-T6 | -0.141 | -0.6908 | -0.118 | -0.586 | 9.686 | 669.34 | 7.3889 | 320.53 |
| SAE 1045 | -0.183 | -0.5446 | -0.1855 | -0.548 | 3.779 | 446.1 | 3.110 | 402.08 |
| AISI 304 | -0.234 | -0.510 | -0.216 | -0.472 | 4.041 | 247.8 | 4.405 | 448.26 |
| Haynes 188 | -0.170 | -0.818 | -0.613 | -0.801 | 3.552 | 719.2 |
3.653 | 1685.4 |
| Inc 718 | -0.127 | -0.844 | -0.134 | -0.896 | 12.53 | 6573.7 | 11.26 |
8930.2 |
List of upcoming graphs:
1% Cr-Mo-V Steel (Upper and lower life limit)
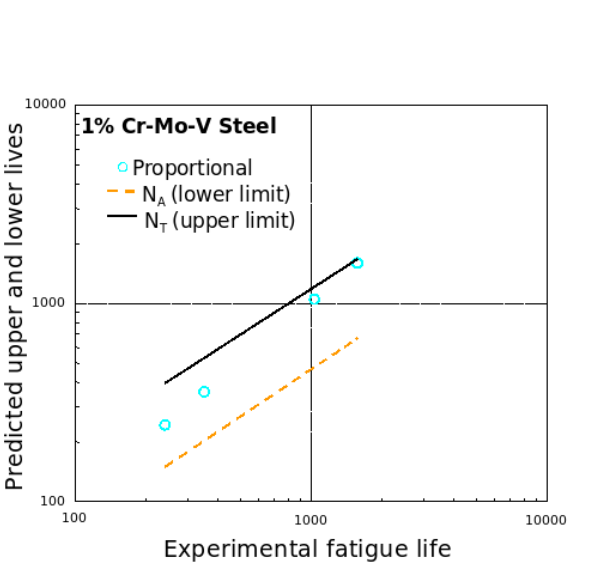
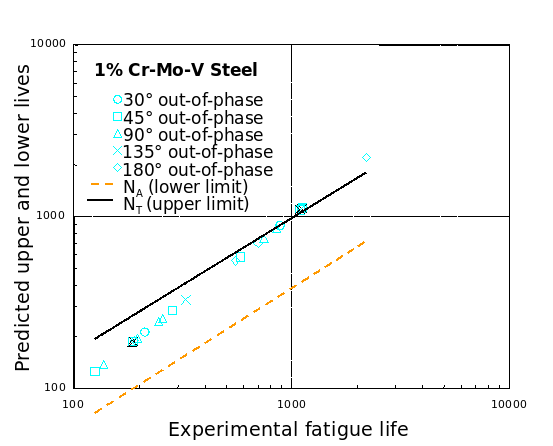
AL7075-T6
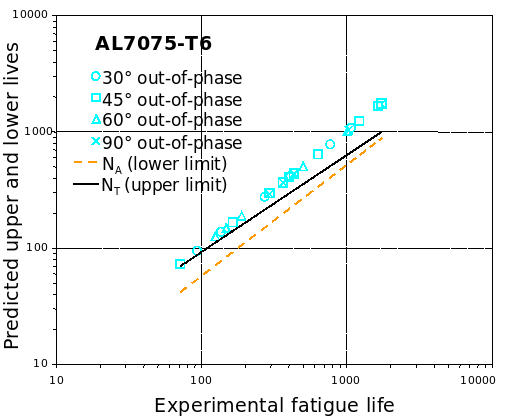
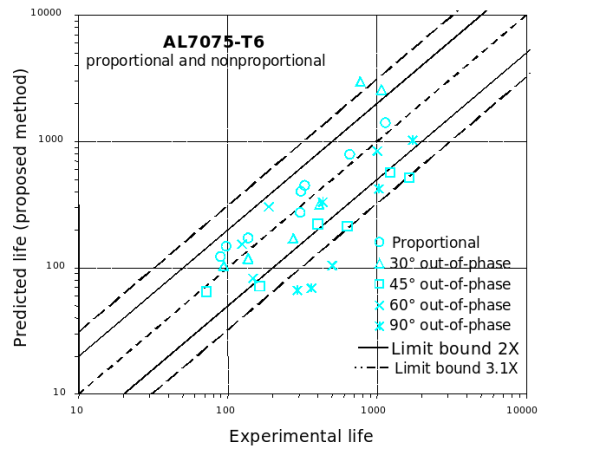
SAE 1045
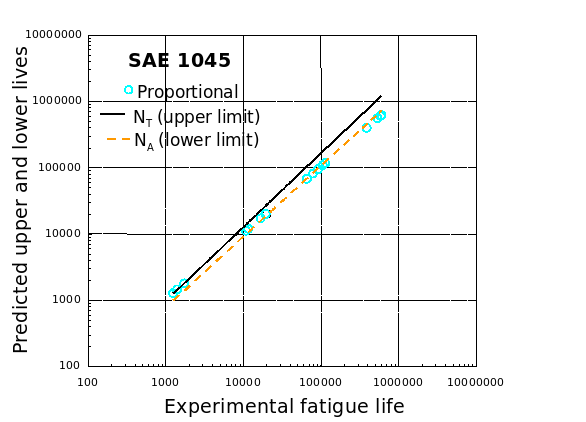
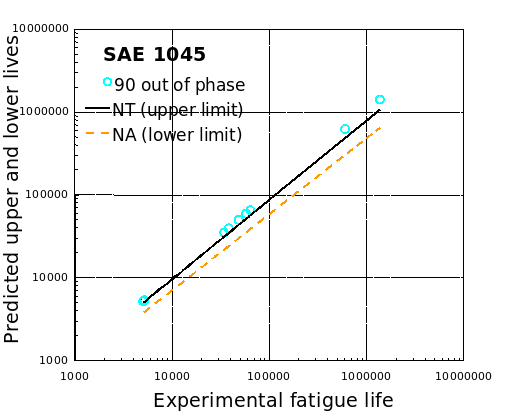
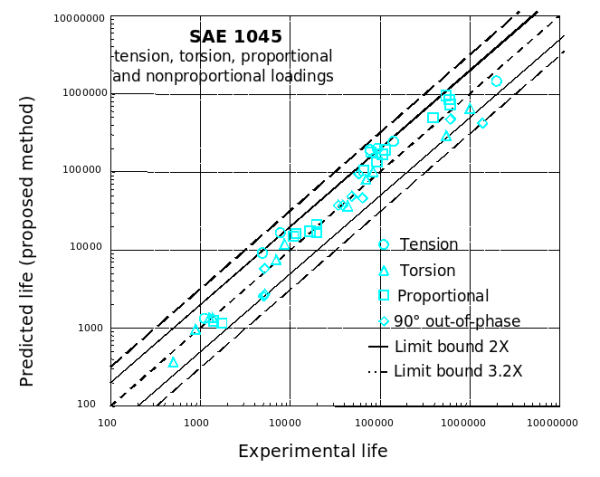
AISI 304
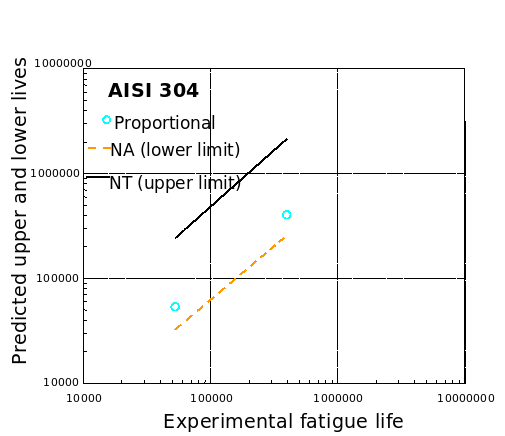
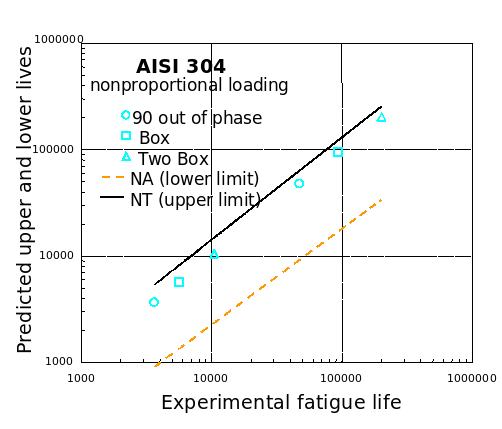
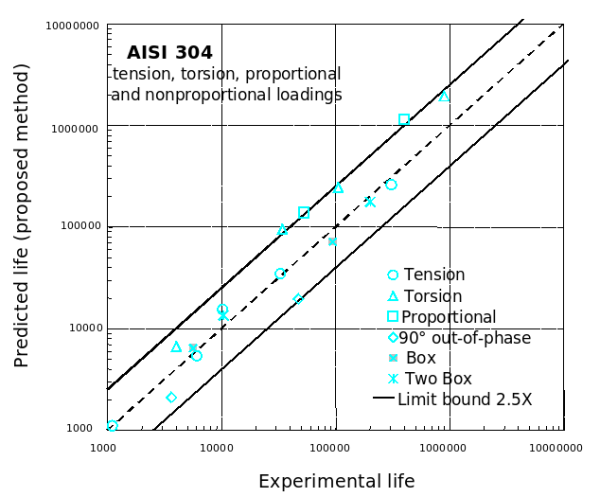
Haynes 188
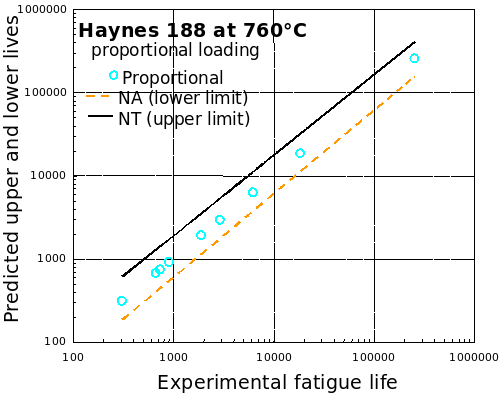
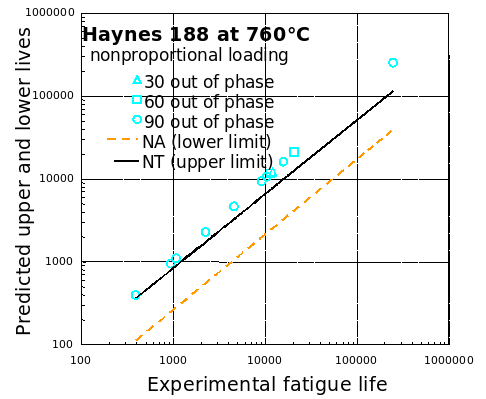
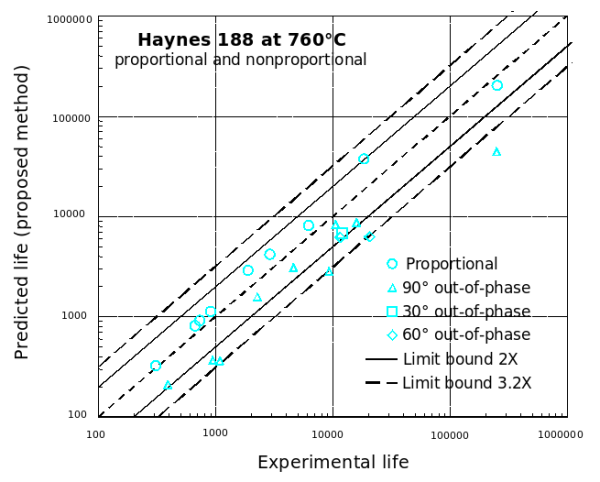
Conclusion
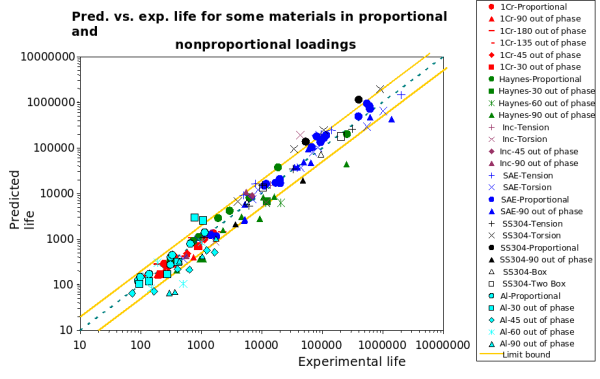
For
more
information
about
experimental
data
refer
to
the
reference
2.
References:
-
Noban M, Jahed H, Varvani A, “The choice of cyclic plasticity models in fatigue life assessment of 304 and 1045 steel alloys based on the critical plane-energy fatigue damage approach,” International Journal of Fatigue, 43 (2012) 217–225;
-
Noban M, Jahed H, Ibrahim E, Ince A, “Load path sensitivity and fatigue life estimation of 30CrNiMo8HH,” International Journal of Fatigue, 37, (2012), Pages 123-133;
-
Noban, M., Jahed, H., Winkler, S., Ince, A., “Fatigue characterization and modeling of 30CrNiMo8HH under multiaxial loading,” Materials Science and Engineering A 528 (6), (2011), 2484-2494;
-
Jahed H, Noban M, " Fatigue of Electroformed Nickel ", Journal of Failure Analysis and Prevention, J (2009) 9:549–557
- Jahed H, Varvani-Farahani A, "Upper and lower fatigue limits calculation using energy- based fatigue properties", Int Jnl Fatigue 2006;28:467-473
- Jahed H, Varvani A, Noban M and Khalaji I, "An energy-based fatigue life assessment model for various metallic materials under proportional and non-proportional loading conditions", Int Jnl Fatigue 2007;29:647-655