Modelling and simulating microorganism locomotion
The fluid mechanics of swimming microorganisms has been studied since the 1950s [1,2]. Flagella of bacteria and spermatozoa are long and thin, motivating the development of approximate analytical treatments of the hydrodynamic problem now known as resistive force theory (RFT) and slender body theory [3,4]. Since long range hydrodynamic interactions between different sections of the filament are not taken into account, RFT is quantitatively inaccurate in many applications [4–6] but remains popular in mathematical models due to analytical tractability [7,8].
More accurate and general numerical approaches, such as the boundary element (BEM), regularised Stokeslet, and immersed boundary methods (IBM), have also been applied to the hydrodynamics of microorganisms [9–13]. Many microorganisms use slender flagella for motility. Although there are important differences between bacterial flagella and those of eukaryotic cells (e.g., spermatozoa and euglenids), they can be simulated with the same numerical approaches. The key differentiating factors among species are the morphology and model for beat patterns, or swimming gaits.
The most detailed models of the mechanics of bacterial flagella consider an energy functional that depends on bending and twist along the filament and has multiple local minima, corresponding to different helical conformations observed in bacterial flagella [14,15]. These models could be used to shed light on the mechanical implications of the wide variety of propulsion systems found in microorganisms, a fundamental question that has been addressed only superficially in the literature.
Below are some areas of interest within this general field.
Development of numerical methods
Models and numerical schemes for simulating the swimming of flagellated organisms have already been developed [6,16–18]. There is, however, still room for improvement in the efficiency of our numerical methods. In particular, models that account for flexibility of the flagella require very short time steps due to the stiff system of differential equations resulting from the elastic responses. Another aspect to improve is the calculation of accurate hydrodynamic interactions, which are nonlocal, in an efficient manner that can be scaled up to simulate multiple (possibly large numbers of) swimmers.
Bacterial motility
Most of our published work has been on bacterial locomotion. Focusing on monotrichous (single flagellum) models, we established the effects of geometric parameters of the cell body and flagellum on swimming efficiency and the tendency of such model swimmers to be attracted to no-slip surfaces [19]. We initially considered rigid flagellum models and have recently extended studies to models with multiple flexible flagella. Using these models, we can address many challenging questions about experimentally observed behaviour of bacteria and the diversity of morphologies and modes of swimming.
For example, some bacteria have a single flagellum whereas others have two or several flagella, which can be located at specific sites on the cell body or distributed randomly. Various motility patterns, such as run-and-tumble, run-reverse, run-flick-reverse, and run-reverse-flick, have been reported for different species [20]. These patterns can be studied and compared systematically through simulations to understand their differences.
Bacterial flagella are typically modelled using Kirchhoff rod theory with a linear constitutive equation. It has been shown, however, that small changes in the configuration of the molecular units forming the flagellum give rise to different helical shapes and that transitions these conformational states can occur depending on environmental conditions and mechanical stresses [14,15,21]. This so-called polymorphism is evident when the motors reverse direction during tumbling events, for example. Modelling these dynamic transitions requires modifications of the constitutive equation for the elastic rod.
Selected publications:
- H. Shum, E. A. Gaffney, and D. J. Smith, Modelling Bacterial Behaviour Close to a No-Slip Plane Boundary: The Influence of Bacterial Geometry, Proc. R. Soc. A 466, 1725 (2010), doi: 10.1098/rspa.2009.0520.
- H. Shum and E. A. Gaffney, The Effects of Flagellar Hook Compliance on Motility of Monotrichous Bacteria: A Modeling Study, Phys. Fluids 24, 061901 (2012), doi: 10.1063/1.4721416.
- H. Shum, Microswimmer Propulsion by Two Steadily Rotating Helical Flagella, Micromachines 10, 65 (2019), doi: 10.3390/mi10010065.
- V. Nourian and H. Shum, A numerical method for the locomotion of bi-flagellated bacteria in viscous fluid, Flow 3, E4 (2023), doi: 10.1017/flo.2022.34.
Active droplets and squirmers
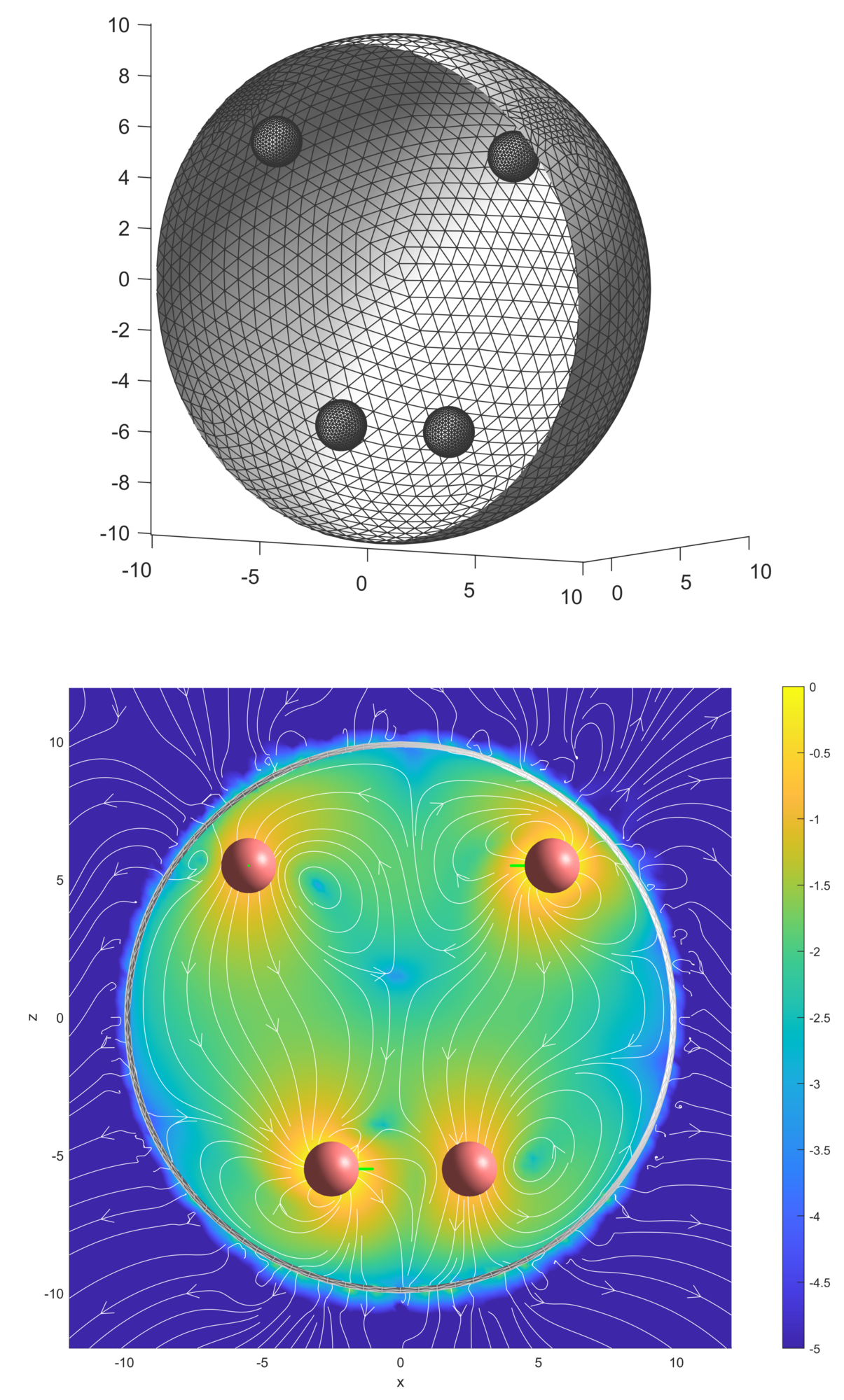Suspensions and mixtures in which chemical or biological activities, such as reactions, dissolution, and swimming take place are termed active fluids. An example is an emulsion of oil droplets added to a concentrated surfactant solution, which gradually dissolves the droplets. During this process, gradients in concentrations around the droplets lead to Marangoni stresses that generate observable fluid flows and can propel the droplets through the fluid. Suspensions of such droplets experience hydrodynamic and chemical interactions. We model the active droplets as spherical squirmers [22] of neutral, extensile, or contractile type. This model assumes that a particular velocity distribution can be generated over the surface of the sphere by an unspecified mechanism, making it a popular generic model for studying self-propulsion and fluid flows driven by active particles. We use boundary element simulations to numerically study these systems.
Collaborators: Bryan Quaife (Florida State University), Sangwoo Shin (University at Buffalo), Yuan-Nan Young (New Jersey Institute of Technology)
Sperm motility
According to the Government of Canada, roughly 1 in 6 couples in Canada experience infertility and a significant portion of these cases are due to low sperm count or low sperm quality, which includes abnormal shapes and low motility. Studying how sperm swim in fluids of different rheological properties and confined environments could help us understand the natural process and the precise reasons for failure in abnormal sperm.
Most theoretical models of sperm assume specific kinematics or a preferred beat pattern. An open question is how the thousands of molecular motors in the flagellum are regulated to produce a beat pattern [23,24]. Models can also be used to probe the motor activity based on experimentally observed kinematics [25].
Euglena motility
Euglena gracilis and other euglenids have more complex, poorly understand flagellar beat patterns [26]. They also use a different mechanism for motility called metaboly [27], in which the cell body undergoes a sequence of deformations to move forward or turn. The mathematical framework for describing propulsion due to body shape changes is well established [28] but the regulation of these shape changes and flagellar beats is poorly understood, particularly when the organism is responding to confined environments.
Collaborator: Dan Nicolau (McGill University)
Microrobots
We investigate the performance of bio-inspired microrobotic swimmers in various environments [29–32]. Robots should be designed with simple actuations, i.e., with a minimal set of controls, but should be controllable [8,33,34] and swim efficiently. A major challenge in microrobotics is how to design them to be either autonomous (e.g., able to seek a particular stimulus or act cooperatively in swarms) or easy to control independently with external guidance (such as magnetic fields).
Controllability of multi-particle systems in Stokes flow
Due to the linearity of the equations of Stokes flow, the velocity of a particle can be expressed as a sum of contributions from the background flow field, external forces acting on the particle, and the flow field generated by the motion of other particles. Approximate formulas are known for the hydrodynamic coupling between spherical particles. With these approximations, we can formulate relatively simple systems of equations governing the dynamics of a collection of particles and study controllability problems. For example, is it possible to move any number of particles from arbitrary starting positions to arbitrary target positions by exerting forces or torques on a separate set of particles? Or, can artificial cilia be actuated to achieve the same goal of transporting particles to arbitrary target positions? If so, such techniques could be used in microfluidic devices for controlling transport and microfabrication.
Collaborators: Marco Morandotti and Marta Zoppello (Politecnico di Torino)
Population-level modelling of microorganism transport
Most of our simulations of microorganisms so far have dealt with deterministic motion of a single swimmer in the presence of planar surfaces. We can build stochastic models to describe the spread of a population of swimmers in more complicated geometries using detailed simulations guide the rules for how swimmers behave in various situations. By relating the statistical properties of the results from stochastic models to the rules we encode, we can determine the effects of subtle differences in morphology or motility patterns on the population behaviour.
These models can be compared with experimental data for organisms placed in mazes and other environments [35–37].
Collaborator: Dan Nicolau (McGill University)
Spatio-temporal patterning of chemicals and fluid flow
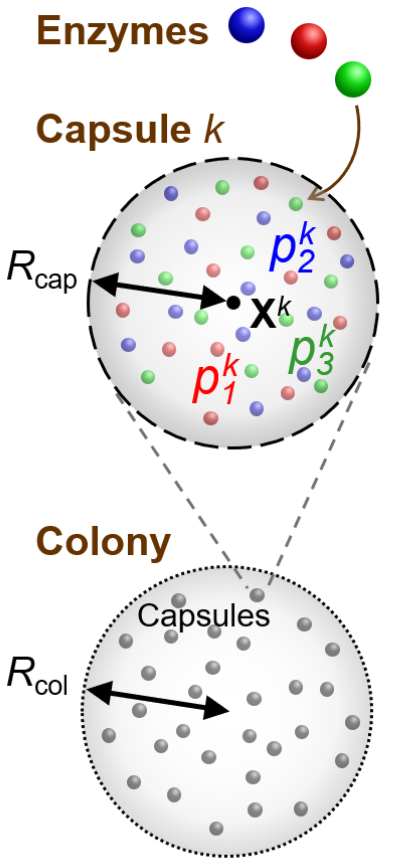
Living organisms have developed astounding functionality and complexity, all arising from chemical reactions and physical phenomena. Our aim is to model physico-chemical interactions among artificial cells that give rise to emergent spatial organisation and collective motion. Experimentally, spherical vesicles have been made with phospholipid or polymeric membranes [38,39]. Vesicle diameters from 50 nm to 1 mm can be achieved [40] and properties of the membrane, such as rigidity and permeability to small molecules, are tuneable [41]. Encapsulated enzymes and DNA allow programmable reactions or metabolism to be carried out [42], achieving such functions as motility [43], intercellular signalling [44], and stimulus-triggered cell rupture [45].
Our focus is on modelling abstract regulatory networks used to modulate the production of various types of chemicals, which perform a range of functions in biological cells: intercellular signaling, mediating adhesive interactions, or generating mechanical stress, for instance. Such functions will be crucial for organising artificial cells into complex “organisms”. We will also combine chemical reaction networks with hydrodynamics and fluid-structure interactions to study autonomous control of motile artificial cells using feedback from mechanosensing by flagella and cilia [46,47].
We have previously studied the repressilator network and demonstrated that it can give rise to self-regulated migration and quorum sensing characteristics in collections of artificial cells [48,49]. We can investigate further to determine how to refine the sensitivity while preserving robustness to parameters that are difficult to control precisely.
We are also interested in patterns spontaneously emerging in chemical systems via diffusion driven instabilities (Turing patterns) [50,51]. It has been suggested that carefully designed reaction systems involving synthetic DNA molecules could be used to program arbitrary, complex patterns in a modular approach [52]. Such patterns can subsequently be used to generate complex patterns of fluid flow.
Selected publications:
- H. Shum and A. C. Balazs, Synthetic Quorum Sensing in Model Microcapsule Colonies, Proc. Natl. Acad. Sci. USA 114, 8475 (2017), doi: 10.1073/pnas.1702288114.
- H. Shum, V. V. Yashin, and A. C. Balazs, Self-Assembly of Microcapsules Regulated via the Repressilator Signaling Network, Soft Matter 11, 3542 (2015), doi: 10.1039/C5SM00201J.
