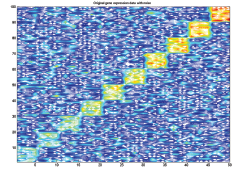
Convex optimization is powerful tool for solving problems in data science.  Efficient algorithms can be brought to bear, and duality opens the door to analysis of the optimizer to establish that it solves the original application. My students and I have applied convex optimization to unsupervised machine learning problems of clustering, nonnegative matrix factorization, and the disjoint communities problem.

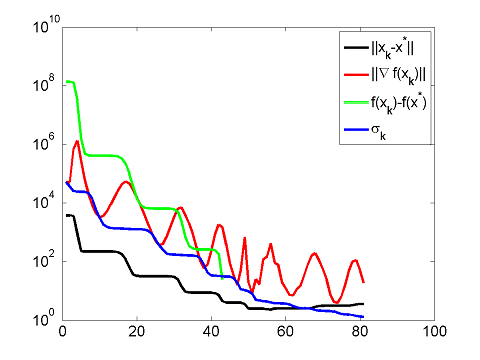
First order methods solve optimization problems using first-derivative information.  Several "optimal" methods such as conjugate gradient, accelerated gradient, and geometric descent have been proposed.  Our recent work shows these methods have a unifying analysis.  This leads to the development of new and more efficient algorithms.

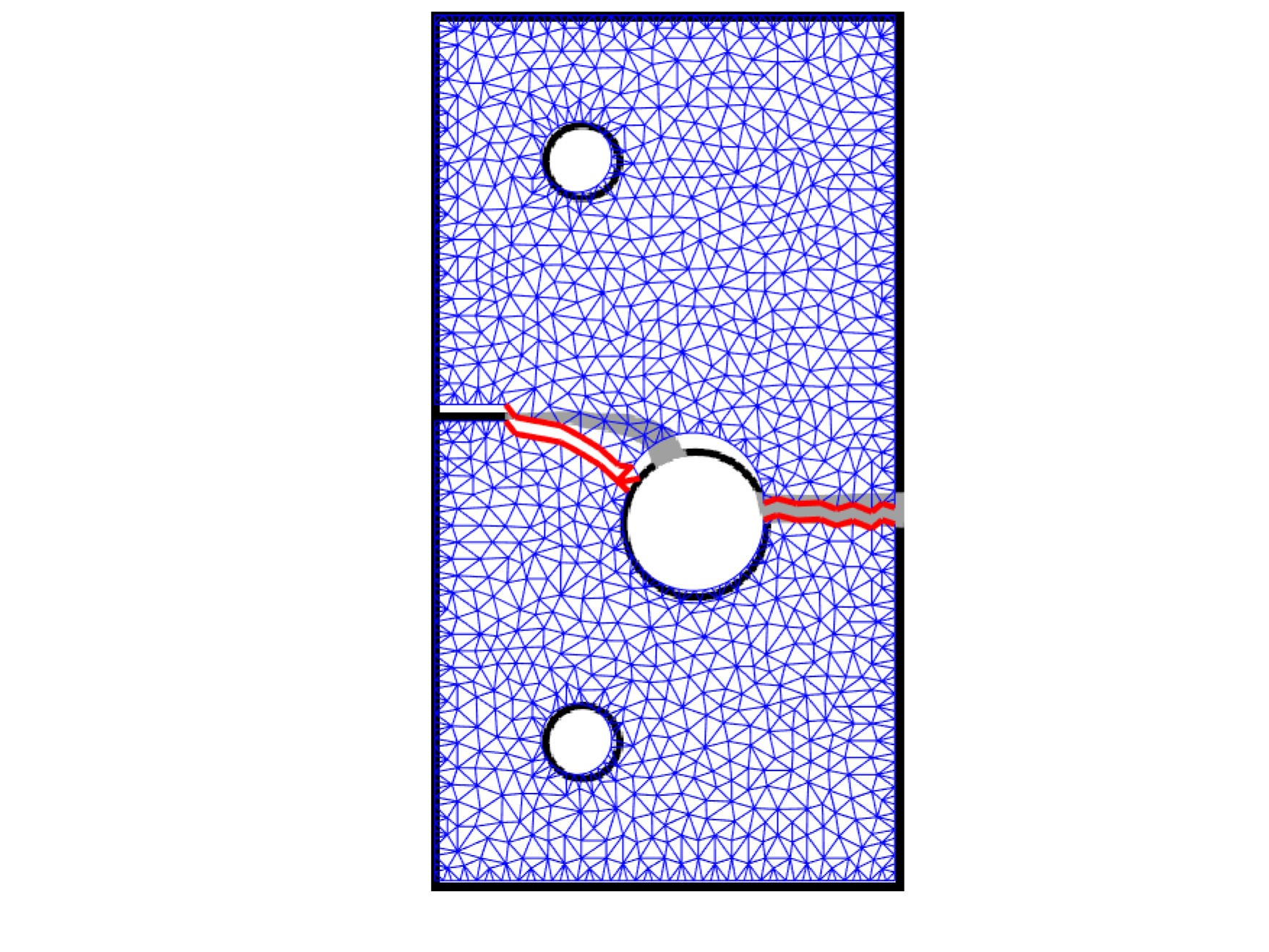
With colleagues and students, we are applying modern and powerful optimization techniques to fracture mechanics of solids. The main point is that fracture can be regarded as an energy minimization process, and hence is amenable to optimization.  We are currently investigating new methods of machine learning for this problem.