
Cellular Automaton
by Amy VanderLaanConway's Game of Life
Conway’s Game of Life was created in 1970 by British mathematician John Horton Conway. It involves cellular automaton, a discrete model of computation consisting of a grid of cells in which each cell is one of two states: dead or alive. The cellular automata concept was originally developed in the 1940s by Stanislaw Ulam and John von Neumann as a way to model self-replication. Conway’s Game of Life helped create interest in the subject beyond the world of academia.
The gameplay is simple, you select which cells to set as alive, hit play, and see what patterns are created! The neighbourhood of any cell is made up of the 8 cells that surround it. Cells live or die based on the following rules:
- A live cell dies if it has fewer than two live neighbours
- A live cell with two or three live neighbours lives on to the next generation
- A live cell with more than three live neighbours dies
- A dead cell with exactly three live neighbours becomes a live cell
You can try it for yourself using one of many online emulators, such as ConwayLife.com. Or type "Conway's game of life" into Google and look to the right of your screen for a little surprise!
Common Patterns
Below are some common patterns that appear in the Game of Life. This includes still lifes - patterns that are stationary, oscillators - patterns that return to their initial state, and spaceships - patterns that move across the grid.
See if you can make any of these patterns appear:
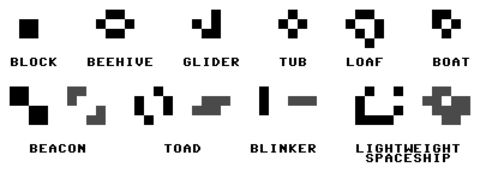
Common patterns in the Game of Life
AI Event

Conway's Game of Life on a Commodore 64C at the AI Event
Conway's Game of Life in Action

We used a Commodore 64C to run a simulator of Conway's Game of Life, made by Marek Karcz. You can visit our office in DC 1316 to try it!
About the Author
Amy studies Computational Mathematics at the University of Waterloo and is the Computer Museum’s Fall 2024 co-op student. In her free time, she enjoys painting, collaging, and other forms of visual art making.



