by Ayoung Eun and Charlotte Wipp
What is this exhibit?
Parts of a Slide Rule
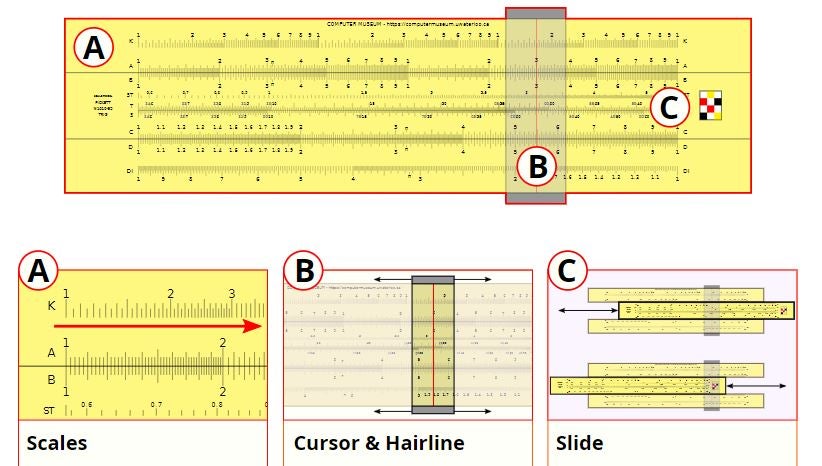
University of Waterloo Computer Museum. Parts of a Slide Rule. 2024.
The Rise and Fall of Slide Rules
Scottish mathematician John Napier developed logarithms in the early 17th century. He also used logarithms to create physical numbering rods known as “Napier’s bones” that simplified multiplication and division of large numbers. However, it was English mathematician William Oughtred who first combined different logarithm scales in the 1620s to create the small, portable, analog computing devices known as slide rules to speed up and simplify various arithmetic operations.
Over time, the popularity of slide rules increased, and they were standard equipment for many occupations. The slide rules that you can see in many of our artifacts used scales meant for general-purpose arithmetic and trigonometry calculations, but many slide rules with different scales were created for specific users such as doctors, engineers, or pilots.
In the mid-1970s, the arrival of portable electronic calculators decreased demand for slide rules. Although the first digital calculators were very expensive and could cost hundreds of dollars, prices fell quickly and by the end of the decade the electronic technology had replaced slide rules as the mathematical tool of choice for almost everyone. The new pocket-sized devices contained microprocessors, and some could be programmed by users to include different mathematical functions. Some calculators, like the Texas Instruments SR-52, could even save short programs to small magnetic cards for later use.
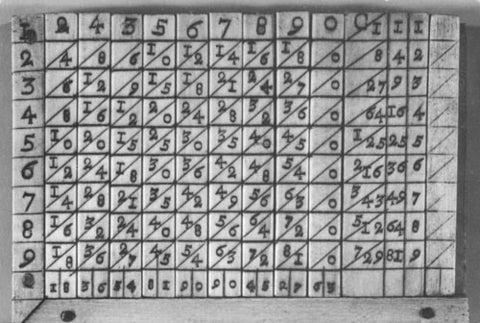
An example of the Napier's bones calculating tool which performs multiplications and divisions by addition and subtraction.
Parts of a Slide Rule
The slide rule is made of several parts: the top and bottom body and the movable slide in between. Both the body and slide contain scales.
The hairline is the movable, clear part. It is used to align values and improve usability.
Many different scales can be used on a slide rule. Some are common, and some are tailored to a specific use or profession. Here is a list of some common scales and their uses:
-
A and B: Scales of squares.
-
These scales have the squares of the D and C scales and can also be used for square roots. The first half of the scale represents 1-10, and the second from 10 to 100, although the significant digits are not on the scale and must be handled mentally.
-
In the first photo to the right, A and B scales are highlighted in blue, while the D and C scales are in green.
-
-
C and D: Fundamental scales.
-
Many of the primary slide rule calculations are done with the C and D scales, which run from 1-10 in a standard log scale format.
-
The D and C scales are highlighted in blue.
-
-
CI and DI: Reciprocal scales.
-
These scales are helpful to simplify division and if the slide extends far past the body.
-
The DI and CI scales are highlighted in blue in the photos.
-
-
E: Log-log scale.
-
The scale for exponential powers. On some rules it is known as the LL3 scale.
-
The exponential scales are highlighted in blue
-
-
K: Scale of Cubes.
-
The scale can be used for cubes and cube roots. It is divided into three sections: 1 to 10, 10 to 100, and 100 to 1000. Like the A scale, significant digits are not on the scale and must be handled mentally by the user.
-
The K Scale is highlighted in blue while the D scale is highlighted in green
-
-
L: Log scale.
-
A linear, non-logarithm scale, often used with C and D scales to determine the logarithmic relation to log base 10.
-
The L Scale is highlighted in blue, while the C and D scales are highlighted in green.
-
-
S: Sine and cosine scale.
-
The scale often presents cosine as decreasing and sine as increasing and usually presents angles from 5.7 to 90 degrees.
-
The S Scale is highlighted in blue
-
-
ST: Sines and tangents scale.
-
The scale exists to work with smaller angles in the range of 0.57 to 5.7 degrees. This scale is used with the C and D scales for values between 0.01 and 0.1.
-
The ST Scale is highlighted in blue
-
-
T: Tangent and cotangent scale.
-
The scale typically ranges from 5.7 to 45 degrees, although sometimes the scale includes values up to 84.5 degrees which run along the bottom in the opposite direction.
-
The T Scale is highlighted in blue
.
-
Scales
More Scales
W.H. Breithaupt's Slide Rule
William Henry Breithaupt was an engineer, entrepreneur, and community leader. First educated in Berlin, Ontario (now Kitchener),his engineering career began in the 1880s, as he worked across the American Midwest, designing railway bridges and tunnels. A cylindrical slide rule such as this one would have been enormously useful for scientific and financial calculations. In 1901 he returned to Waterloo to help manage his family's local businesses and build the first electric railway in the region. He also helped found the Waterloo Historical Society and Grand River Conservation Authority. He is an inductee of the Waterloo Region Hall of Fame.
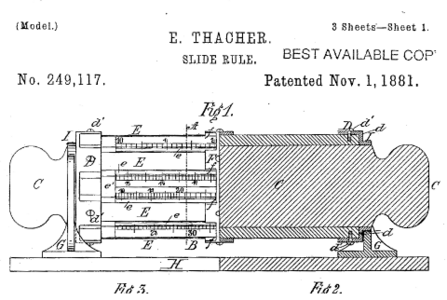

Keuffel & Esser slide rule
Edwin Thacher's 1881 patentdescribes a slide rule small enough to fit on a desk, but much more precise than a normal one the same width. Keuffel & Esser of New Yorkbegan making Thacher-style slide rules around 1887.
What Came After the Slide Rule?
In the mid-1970s, the arrival of portable electronic calculators decreased demand for slide rules. The new pocket-sized devices contained microprocessors, and some could be programmed by users to include different mathematical functions. Some calculators, like the Texas Instruments SR-52, could even save short programs to small magnetic cards for later use.
There are more Slide Rules to see!
Make Your Own Slide Rules!
Print this page out and follow the instruction to create your own Slide Rules. Note that you can download them as PDF.

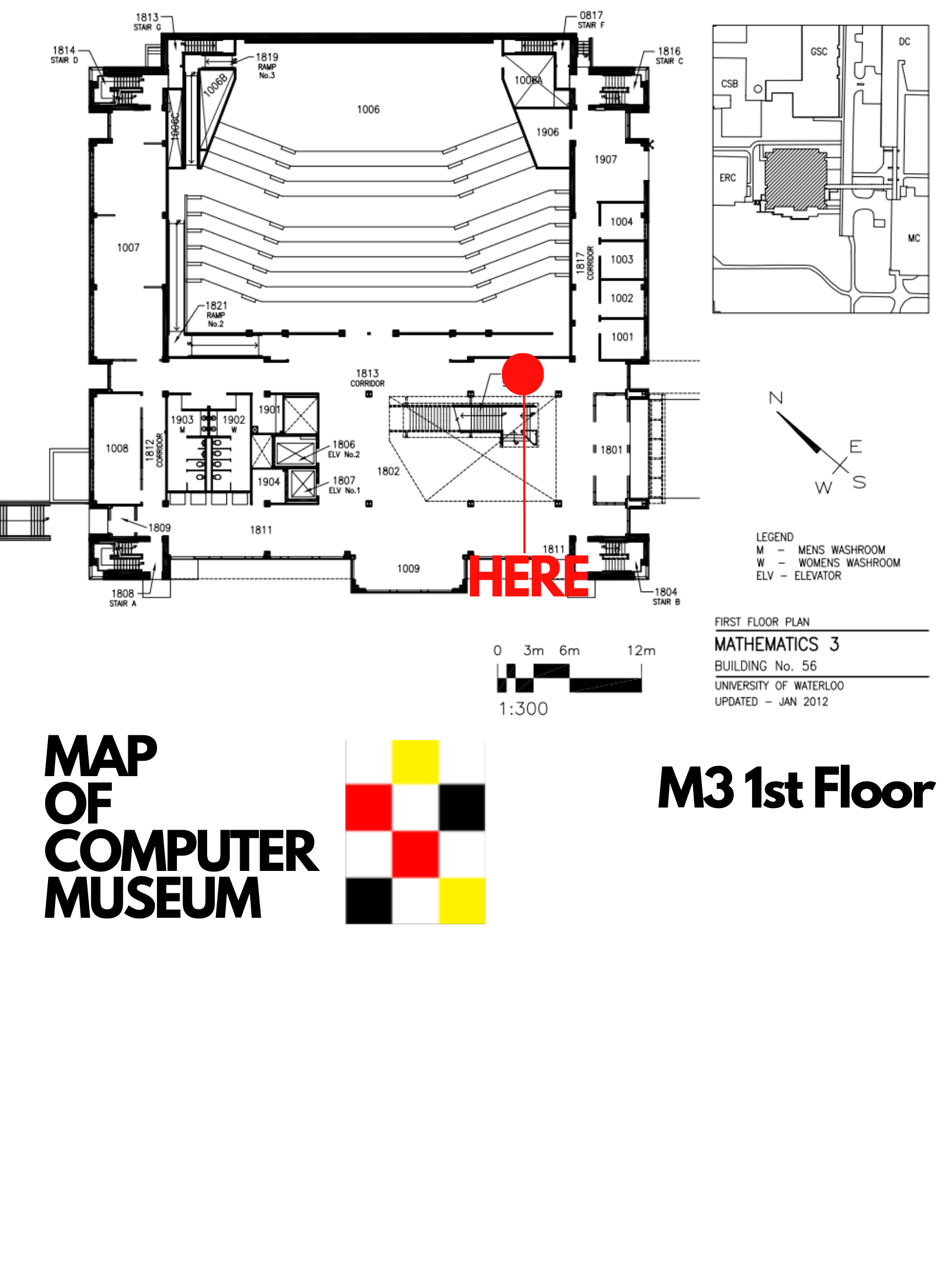
Where are we located?
Have a closer look at the building!
Our Slide Rules exhibit is located inside M3, on the 1st floor. Here is our map:
And here's a sight that will welcome you when you get there:













































































