Any cubic crystal structure can be divided into small units in the form of congruent semi-regular (Archimedean) truncated octahedra. The centers of these polyhedra can be chosen at invariant equivalent positions for most cubic space groups. The part of a crystal structure enclosed by an Archimedean polyhedron is called a geometric unit (or unit for short); however, the boundary of the unit may be relaxed to include a whole molecule or ion in case the geometric division is not convenient. Based on the properties and arrangements of such geometric units, there is an interesting relationship among the 36 cubic space groups. All units in a crystal structure of any one of 16 space groups are equivalent. There are 14 space groups to accommodate crystal structures with two types of independent units. Only crystal structures of space groups F23 and F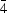3m consist of four types of independent units. The remaining four space groups are in the class with three types of geometric units. The arrangement of geometric units is represented by a sequence of one period along the body diagonals of a unit cell. The sequence of geometric units is a simple version of the packing map on a (110) plane. This packing map reveals structural features.