Citation:
Chieh, C. . (1982). The Archimedean truncated octahedron. III. Crystal structures with geometric units of symmetry m3m. Acta Cryst. (1982). A38, 346-349. Retrieved from https://doi.org/10.1107/S0567739482000722
Abstract:
All geometric units in crystal structures of space groups Im3m and Pm3m and two out of the three types in those of Fm3m have m3m symmetry, whereas the remaining one of Fm3m possesses 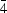 3m symmetry. Theoretically, a geometric unit of m3m symmetry has atoms arranged as a collection of these possible polyhedra: octahedron, cube, cuboctahedron, truncated octahedron, truncated cube, small rhombicuboctahedron and rhombicuboctahedron. All these can be derived from truncations, sometimes repeated, of the pair of platonic solids, cube and octahedron, which possess m3m symmetry. In reality, no known crystal structure has a geometric unit with a rhombicuboctahedron or a truncated cube. The close-packing requirement causes a complicated geometric unit to start (from the center) in one of the following ways: (i) a single atom followed by an octahedron, (ii) a single atom followed by a cube, (iii) an octahedron and (iv) a cube. The survey of structures indicates that polyhedra derived from an octahedron occur more frequently in real geometric units than those related to a cube.
3m symmetry. Theoretically, a geometric unit of m3m symmetry has atoms arranged as a collection of these possible polyhedra: octahedron, cube, cuboctahedron, truncated octahedron, truncated cube, small rhombicuboctahedron and rhombicuboctahedron. All these can be derived from truncations, sometimes repeated, of the pair of platonic solids, cube and octahedron, which possess m3m symmetry. In reality, no known crystal structure has a geometric unit with a rhombicuboctahedron or a truncated cube. The close-packing requirement causes a complicated geometric unit to start (from the center) in one of the following ways: (i) a single atom followed by an octahedron, (ii) a single atom followed by a cube, (iii) an octahedron and (iv) a cube. The survey of structures indicates that polyhedra derived from an octahedron occur more frequently in real geometric units than those related to a cube.