I am interested in flows where stratification is important.
Examples are flows in the lakes, oceans, atmospheres and fires.
I collaborate with faculty members in Applied Mathematics and the MME Fire group to explore these topics.
Some recent projects are listed below
Unsupervised learning to indentify structures in turbulent flows
Coherent structures are ubiquitous in turbulent flows. These structures play a key role in heat and momentum transfer. However, identifying these structures can be difficult as in some cases their characteristics change with properties of the flow. This is where unsupervised methods can help. The goal of these methods is to recognize and learn patterns in large datasets, without a set of ground truth labels. The image below is taken from a direct numerical simulation of a turbulent boundary layer. The blue tones indicate vortical structures while the red tones indicate zones of turbulent production where the structures are identified using an an unsupervised method. We are working on bringing this into more complex architectures that can be used to predict state transitions in stratified turbulent boundary layers
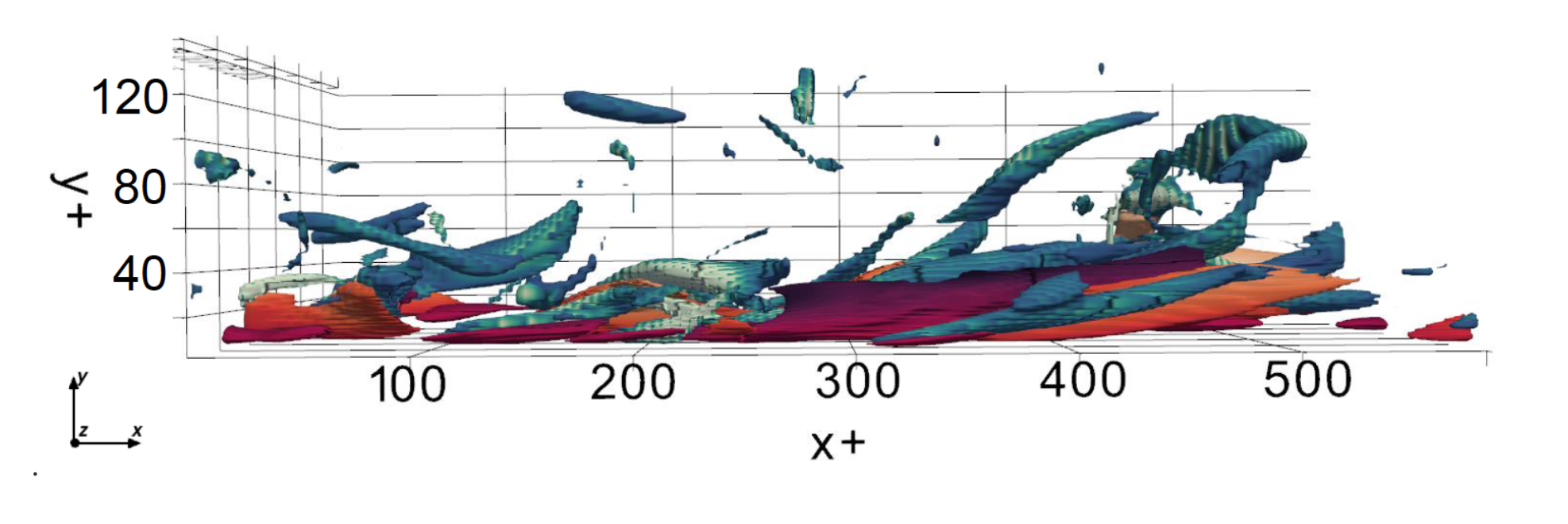
Credit: John Lyne
Stably stratified flows
Stably stratified flows occur in a wide range of environmental and industrial processes. For example, thermal storage tanks and atmospheric boundary layers. They can influence the energy extracted by a wind turbine or the wind load experience by a building. Nocturnal boundary layers are often stable due to radiative cooling, which can help fog formation and slippery conditions that impact driving.
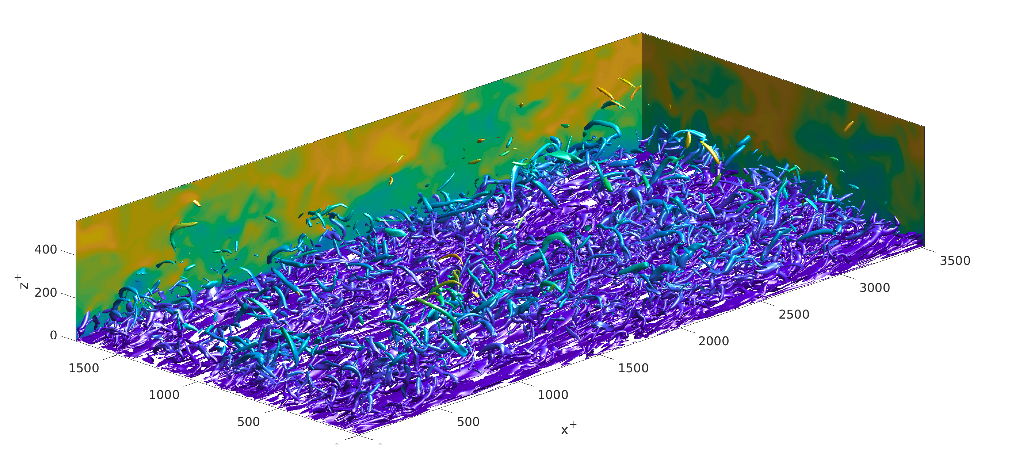
These boundary layers are difficult to capture in forecasting models due to their small scales and intermittent physics. We have been working on improving understanding of the physics of these boundary layers in both transient and steady states using high resolution numerical simulations. Results from these studies can be used for development of better models, We are keen to explore the use of thermal and/or optical imagery to improve our models with data. As an example, below two images from CFD are shown.
Unstratified (no density change) - vigorous mixing
Stratified (denser fluid at the bottom): Mixing is supressed
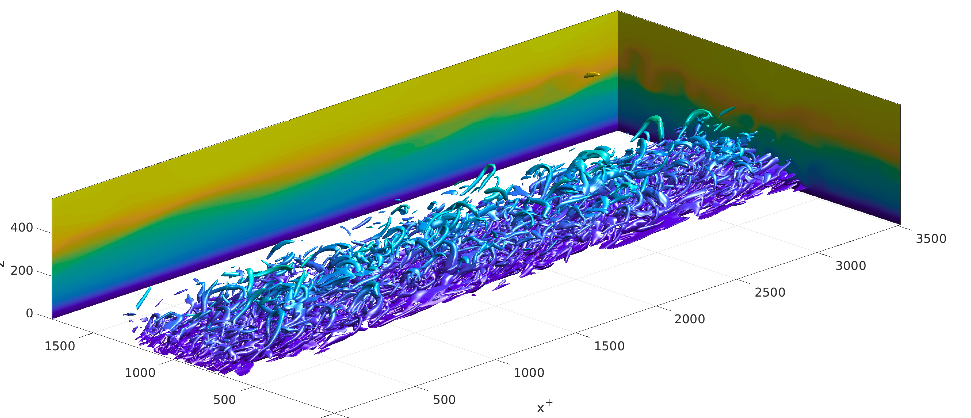
. Credit Amir Atoufi
