Our group uses mathematical modelling tools from systems theory to study biological systems. We combine experiments and computation to investigate biomolecular and intracellular networks. Our current projects are focused on microbial genetics and physiology, and the spatiotemporal dynamics of mixed microbial populations.

Natural biological systems have been selected (through evolution) to perform specific functions. As a result, the study of these systems can be framed as a reverse engineering endeavor. Our work in this area of systems biology involves the development, validation, and analysis of mechanistic mathematical models. These models (typically formulated as systems of nonlinear differential equations or as stochastic processes) represent working hypotheses that allows us to generate predictions about the behavior of systems of interest. These predictions can then be used to refine our understanding and to guide further experimental investigations. In addition to model construction, we are also engaged in the development of new theoretical techniques for model analysis.

Synthetic biology is the forward-engineering of biological systems to achieve desired behaviours. Our work in this area focuses on model-based design, i.e. prototyping by computer simulation, which complements construction and testing in the lab. Our focus here is on the design and construction of gene regulatory networks and the manipulation of microbial population dynamics. A long term goal is the engineering of microbial communities to support improvements in biomanufacturing, health, agriculture, and bioremediation.

Much of our work involves interpretation of experimental data, acquired either in our own laboratory or from those of our collaborators.

A primer on mathematical modelling in systems and synthetic biology is posted here.

Spatiotemporal characterization of interacting microbial populations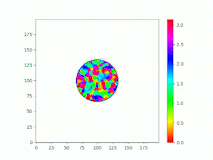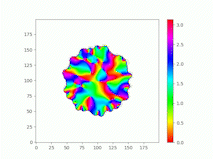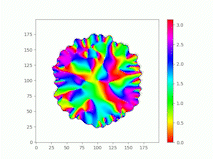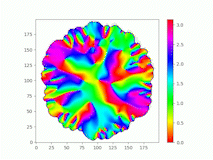

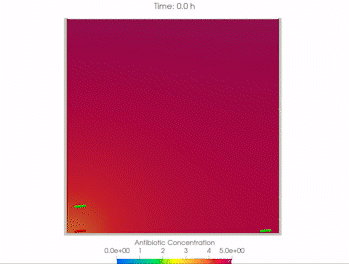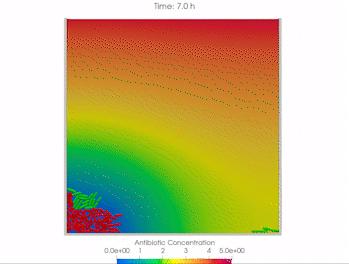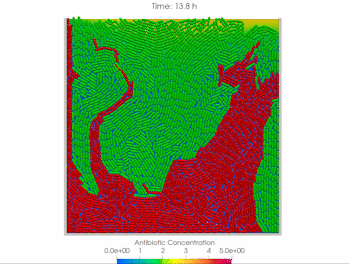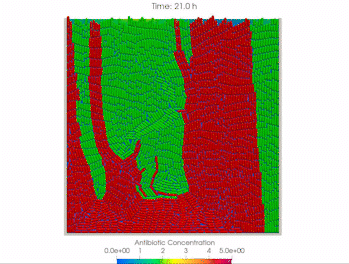
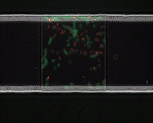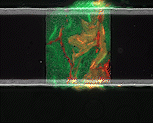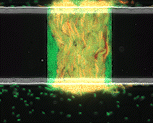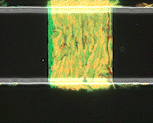
We use time-lapse fluorescence microscopy to observe the spatiotemporal dynamics of mixed microbial populations in constrained and unconstrained environments. Building on our earlier work on non-spatial (ODE) modelling, we are developing spatiotemporal models (PDE and agent-based) to capture the behaviour of populations of cells engaged in various ecological interactions (e.g. antagonism, mutualism, horizontal gene transfer). These models provide quantitative characterization of the dynamics and variability of these populations, and provide a foundation for more complex models that will be useful for predicting the effect of manipulations of mixed populations in the context of, e.g. biomanufacturing, health, agriculture, and bioremediation.

Optimal experimental design tools for model refinement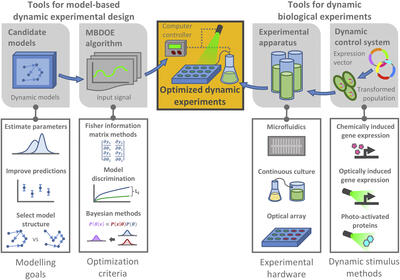
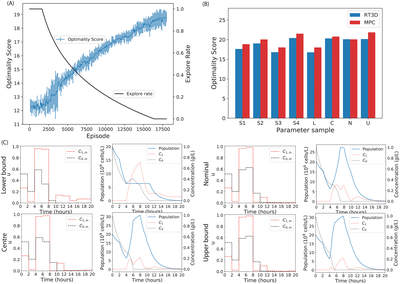Model development and validation typically requires considerable experimental data. The efficiency of data collection can be improved by employing optimal experimental designs, which maximize the informativeness of a given experimental procedure. We are involved in the development and implementation of computational techniques for the identification of optimal experimental designs in the context of modeling intracellular and intercellular processes. Recent results are focused on characterization of bioprocess dynamics and of bacterial genetics and physiology.

Bacteria-mediated cancer therapy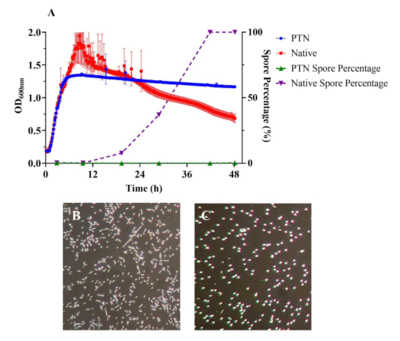
In collaboration with CREM co., we are developing novel approaches to bacteria-mediated cancer therapy. This strategy relies on the fact that obligate anaerobes offer a natural solution to the problem of specificity in cancer therapy: the interiors of solid tumors provide a unique environment in which such populations can propagate. We are engineering a strain of Clostridium sporogenes to achieve tunable oxygen tolerance in addition to environmentally-triggered anti-cancer activity.

Deep learning tools for model development and analysis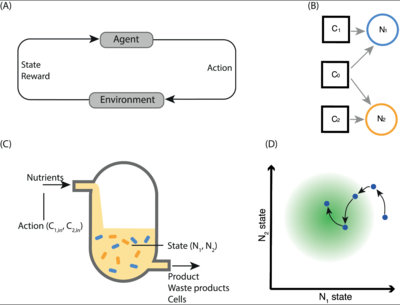
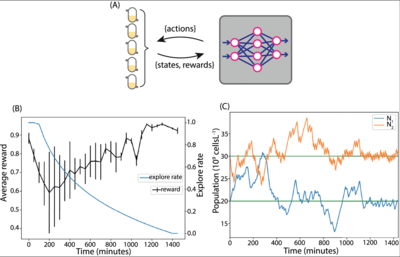Deep learning provides a suite of techniques for analysis and interpretation of experimental data. In collaboration with the Barnes group at University College London, we have developed reinforcement learning algorithms to support bioprocess control and experimental design. Ongoing work involves the application of representation learning for model calibration.

Our work has been supported by

NSERC (Natural Sciences and Engineering Research Council of Canada)

CIHR (Canadian Institutes of Health Research)

CFI (Canada Foundation for Innovation)

MRI (Ontario Ministry of Research and Innovation)

MITACS