Contents
Working with polynomials
A polynomial in MATLAB is represented by a row vector of coefficients. The polynomial:
is represented in MATLAB as:
p = [ 1 -7 11 7 -12 ];
Find roots of the polynomial
The MATLAB command "roots" will provide the roots of a polynomials:
roots(p)
ans =
4.0000
3.0000
-1.0000
1.0000
Define a polynomial by its roots
We can build up a polynomial based on its roots:
r = [1 -1 4 3] poly(r)
r =
1 -1 4 3
ans =
1 -7 11 7 -12
Multiply polynomials
Polynomial multiplication corresponds to Matrix convolution, and so is done using the “conv” command in MATLAB. For example, to compute:
Enter the MATLAB commands:
p1 = [1 -3 1] p2 = [1 0 -1 0 0 -1] conv(p1,p2)
p1 =
1 -3 1
p2 =
1 0 -1 0 0 -1
ans =
1 -3 0 3 -1 -1 3 -1
Polynomial division
Polynomial division corresponds to matrix deconvolution and is performed with the "deconv" command:
num = [1 0 -1 0 0 1] dem = [1 0 -1] deconv(num, dem)
num =
1 0 -1 0 0 1
dem =
1 0 -1
ans =
1 0 0 0
Deconvolution ("deconv" command) can return both quotient and remainder
[q, r] = deconv(num, dem)
q =
1 0 0 0
r =
0 0 0 0 0 1
Evaluate a polynomial at a point
The MATLAB function "polyval" will evaluate a polynomial at a point.
p
p =
1 -7 11 7 -12
polyval(p, 4)
ans =
0
polyval(p, 5)
ans =
48
polyval(p, [1 2 3 4 5])
ans =
0 6 0 0 48
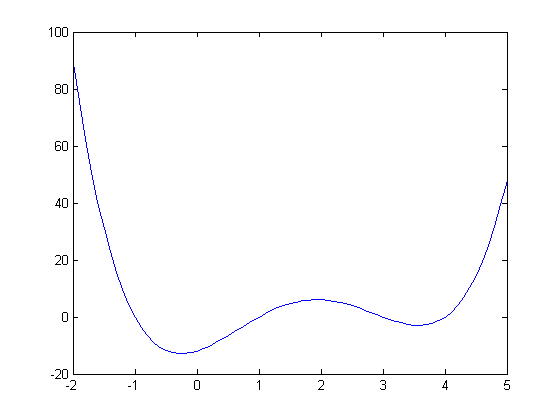
Plot
x = -2:.1:5; plot(x, polyval(p,x))
Exercises
- Use 'polyder' to compute the derivative of a polynomial.
- Use 'polyint' to integrate a polynomial.
- Plot a polynomial and its derivative on the same axis.
- Find the critical points (i.e., roots of the derivative).
- Format plots of the polynomial, its derivative, and/or the critical points.
Published with MATLAB® 7.4