Location
MC 5501
Speaker
Frédérick P. Gosselin, Department of Mechanical Engineering, Polytechnique Montreal
Title
FENNM: A Variational Framework Integrating the Formalism of the Finite Element Method with Physics-Informed Neural Networks
Abstract
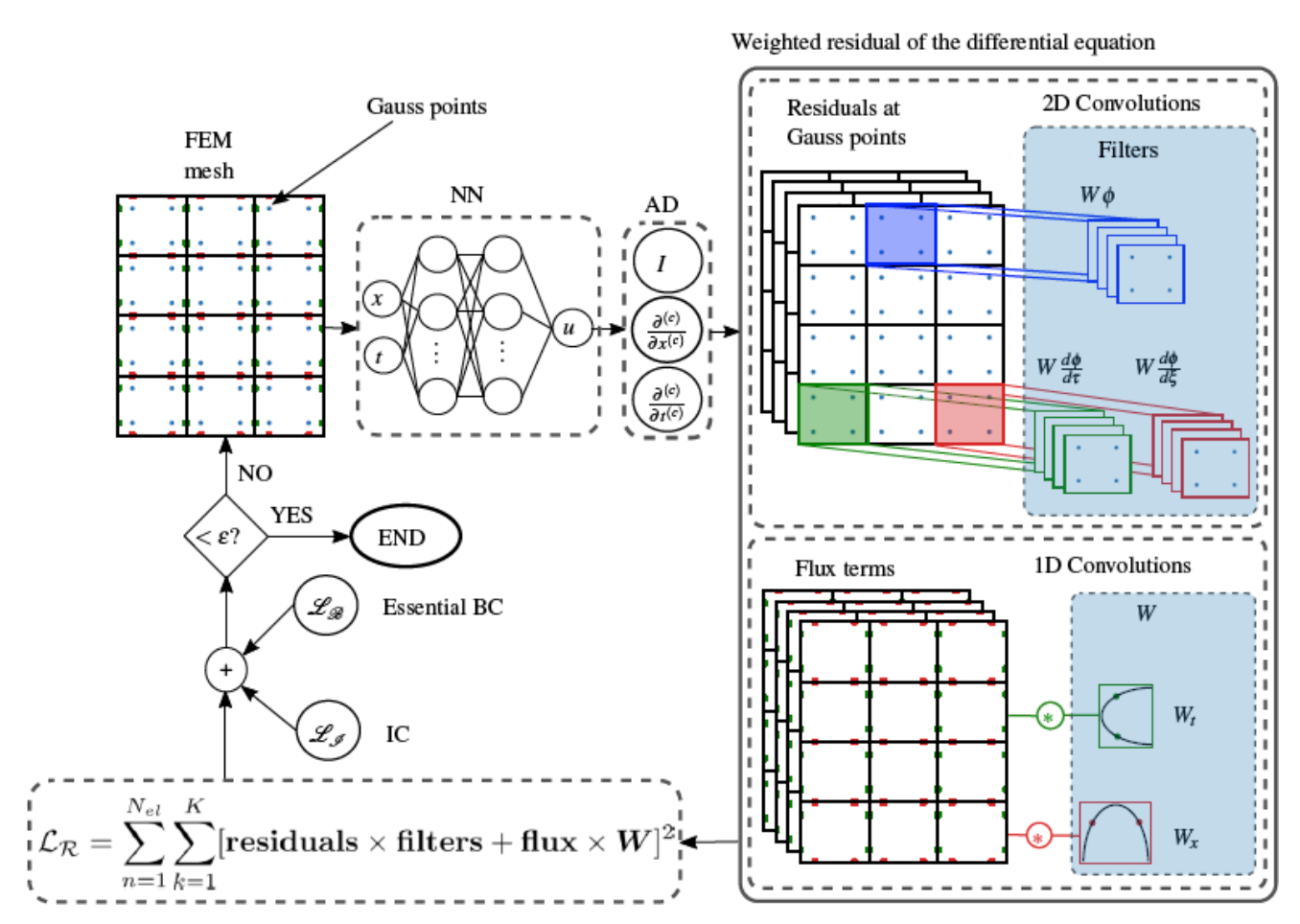
Neural networks (NNs) are increasingly attractive in computational sciences due to their ability to learn complex patterns and provide accurate approximations for intricate systems, leveraging their universal nonlinear approximation capabilities and high expressivity. They have notably be deployed to solve differential equations with or without data as Physics-Informed Neural Networks (PINNs). While conventional numerical methods remain the standard for accuracy and dependability, the research presented in this seminar bridges these paradigms by introducing the Finite Element Neural Network Method (FENNM) to solve partial differential equations.
Based on the Petrov-Galerkin framework, FENNM employs convolution operations to approximate the weighted residual of differential equations. The NN generates the global trial solution, while the test functions belong to the standard finite element method (FEM) shape function space like Lagrange polynomials. FENNM introduces several advantages. Notably, the weak-form of the differential equations introduces flux terms that contribute information to the loss function compared to VPINN, hp-VPINN, and cv-PINN. This enables the integration of forcing terms and natural boundary conditions into the loss function similar to conventional FEM solvers, facilitating its optimization, and extending its applicability to more complex problems. We demonstrate the new possibilities that can be harnessed by combining the finite element formulation with PINNs. We demonstrate the method’s efficacy through numerical case studies involving spatiotemporal 1D and 2D Burgers’ equations, vector-valued Navier-Stokes flows, and the inverse identification of thermal properties in satellite systems. Finally, we illustrate how FENNM seamlessly handles irregular meshes generated by standard tools like Gmsh, bridging the gap between deep learning research and industrial engineering workflows.
Biography

Frédérick P. Gosselin is professor in the Department of Mechanical Engineering at Polytechnique Montreal (appointed 2012) in Canada. He was a visiting professor at the University of Calgary (2025) and the University of British Columbia (2018-19). He studied Mechanical Engineering at McGill University in Montreal (B.Eng. 2004), completed his master’s degree under the supervision of Michael P. Païdoussis (M.Eng. 2006) at McGill and his Ph.D. under the supervision of Emmanuel de Langre at École Polytechnique in France (Ph.D. 2009). He is an expert in slender structure mechanics and fluid-structure interaction. He studies a variety of slender structures ranging from tree leaves, soft corals, and cell membranes to aircraft parts and hydraulic turbine runners. He holds an NSERC Discovery grant to study Morphing Matter Under Fluid Flow: Programming Fluid-Structure Interaction via Bioinspiration. Prof Gosselin actively collaborates with companies involved in the energy sector, such as Hydro Québec (IREQ) and Maya HTT to develop digital twin technologies.