IQC PhD student John Donohue, along with Elie Wolfe from the Perimeter Institute of Theoretical Physics, has determined the required complexity of a quantum system and how many bits of shared classical information are needed between two parties to generate a general probability distribution with a known set of quantum correlations.
Taking a device-independent perspective, without making any assumptions about experimental execution such as measurement devices or other variables, the pair of researchers investigated theoretical quantum systems with a restricted set of inputs and outputs. They looked at how much shared randomness – the length of a shared string of bits or classical information – between two parties is required for the system to fill out the set of quantum correlations. Characterizing this set of possible correlations is useful in classifying what tasks can be done using classical physics and what tasks need quantum resources.
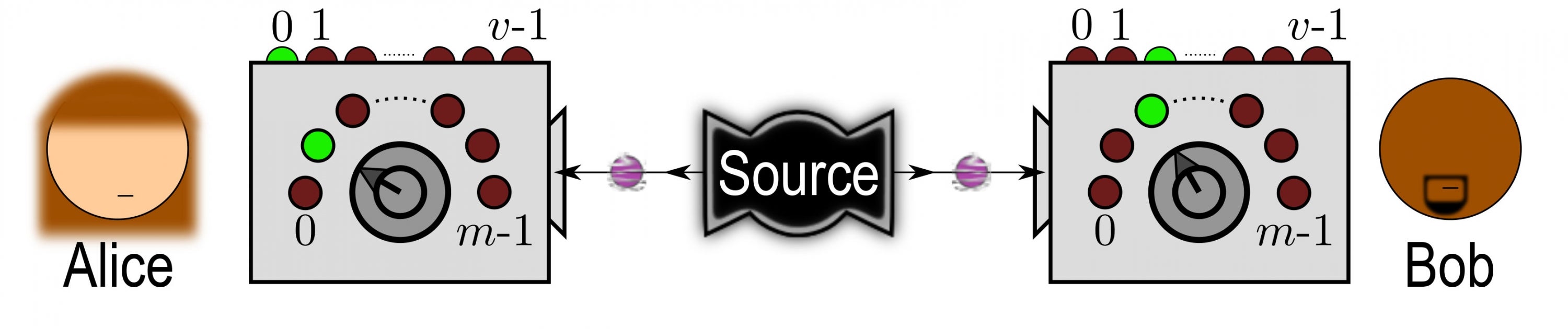
In a device-independent setting, two parties named Alice and Bob, obtain some output after setting a dial to their desired input. This description avoids assumptions about the internal physics of their devices, yet can still be used to verify genuine non-classical (for example, quantum) behaviour through simply the correlation of their outputs.
In a simple case where Alice and Bob can each choose one of two inputs and reveal one of two possible outputs, Donohue and Wolfe found that at most three bits of shared randomness are required to reach the full set of achievable quantum correlations with a two-qubit system. Without this shared randomness, the range of possible quantum correlations is nonconvex, meaning that even if two types of correlation are possible to build, their average may not be. This is the first time that nonconvexity has been shown for complete regions of quantum correlations.
These results may be useful for entanglement verification and opens the door to further research in this area. “Many questions remain,” says Donohue, “including the consideration of more complex scenarios with additional qubits.”
Physical Review A published the paper Identifying nonconvexity in the sets of limited-dimension quantum correlations on December 14, 2015.