One of the tasks that quantum computing promises is algorithmic speedups over classical computing for certain types of problems – one of which is quantum searching. To achieve this, it’s important to build a robust quantum memory, more specifically, a memory that can store information which can be addressed quantum mechanically.
Quantum Random Access Memory (qRAM) acts as a bridge between the quantum computer to the storage system. One important use of qRAM is as an oracle in quantum searching of large databases. The oracle reveals the result of the query. Grover’s algorithm is one algorithm that uses such an oracle for big data mining or quantum cryptanalysis. It allows a quadratric reduction \mathcal{O}\sqrt{N} in the number of queries required compared to the best known classical searching algorithms.
In practice, oracles are noisy and do not always return the correct queried value. The bucket brigade model for implementing qRAM introduced by Giovannetti, Lloyd and Maccone introduced several advantages over the typical fan-out binary-tree approach to these types of queries. One of the main advantages is that it requires exponentially less active, potentially noisy processes to complete these queries allowing for more efficient energy consumption, but more importantly, a more robust implementation.
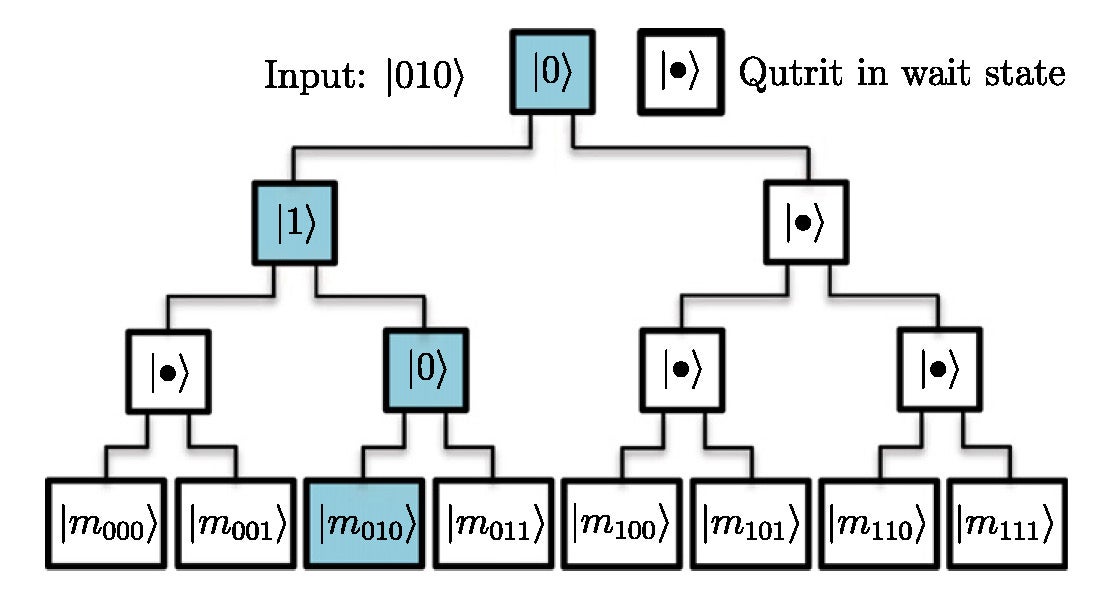
“The bucket brigade model proposed by Giovannetti et al activates routing nodes only along the active path in the computation, it reduces the chances of error and increases the speedup,” said Vlad Gheorghiu, a postdoctoral fellow at the Institute for Quantum Computing (IQC). “It works well for algorithms that make a relatively small number of queries (i.e., polynomial), some of which may be used in quantum machine learning.”
The paper published in the New Journal of Physics, by IQC members Gheorghiu, Tomas Jochym-O’Connor and faculty member Michele Mosca along with colleagues Srinivasan Arunachalam and Priyaa Varshinee Srinivasan, raises new concerns about the advantages of the bucket brigade models model for algorithms using super-polynomial oracle queries, such as Grover’s quantum searching algorithm.
Oded Regev and Liron Schiff initially developed surprising results for a special class of noise models in which the quantum speedup was lost unless the error rate per gate was exponentially smaller. The IQC, Centrum Wiskunde & Informatica and Institute for Quantum Science and Technology team used the simplest form of noise, a bit flip error model, to test the robustness of the bucket brigade model for an algorithm using super-polynomially many queries.
“We found that one way to overcome the Regev/Schiff restriction is to reduce the error rate to sufficiently small levels,” said Jochym-O’Connor, a PhD student in the Department of Physics at the University of Waterloo. “We can decrease the error rate exponentially with quantum error correction, but we need to actively error correct each of the nodes, not just those along the active path.”
For algorithms that make a smaller number of queries such as quantum machine learning, the bucket brigade scheme with a polynomially small error rate is still useful. On the other hand, for the Grover quantum search algorithm, and other algorithms requiring super-polynomially many queries, the greater number of noisy queries and the need for active quantum error correction offset the main advantages of the bucket brigade model approach.
“It is important to know if the practical cost of implementing quantum accessible classical memory is closer to the cost of the same amount of classical memory, or if it’s closer to the cost of full-fledged full tolerant quantum bits,” according to Michele Mosca, a professor in the Department of Combinatorics & Optimization and University Research Chair at the University of Waterloo. “Our work illustrates that for quantum algorithms with many queries to the classical memory, current methods do not allow us to bypass having a similar amount of fault-tolerant computational qubits.”