What is Analysis?

Roughly speaking, analysis deals with approximation of certain mathematical objects--like numbers or functions--by other objects which are easier to understand or to handle. For instance if you want to find out the first few decimals of pi, then you will most likely want to write pi as the limit of a sequence of numbers that you already know how to calculate. Or an example going the other way around: the sequence of factorials n! looks aesthetically pleasing, but in calculations one often needs an approximation of n! which shows more clearly its growth order; such an approximation is given by the classical formula of Stirling,

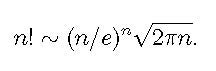
If you had any acquaintance with calculus, then you already know at least one of the major ideas of analysis--differentiable functions are locally approximated by linear ones. One can argue that this idea provided the real starting point of analysis, some three hundred years ago.

But you can be sure that the analysis you study today does not look at all as it did three (or one) hundred years ago. As was the case with other vital branches of Mathematics, analysis has continuously advanced and today has important applications throughout science, engineering and economics. For example, the finance industry has become a significant employer of mathematicians because of the use of analysis.

At present, analysis has accumulated such an enormous body of results that a 'brief review' of the field is literally impossible. Major areas of interest to the analysts in the Pure Mathematics department include real analysis, Fourier analysis (and wavelets), functional analysis, operator theory and algebras, harmonic analysis, probability theory and measure theory. Differential equations is another major area of analysis studied by many applied mathematicians at Waterloo.

Famous people who have made important discoveries in analysis include Newton, Cauchy, Fourier, Hilbert and Halmos.