A form of quantum weirdness is a key ingredient for building quantum computers according to new research from a team at the University of Waterloo’s Institute for Quantum Computing (IQC).
In a new study published in the journal Nature today researchers have shown that a weird aspect of quantum theory called contextuality is a necessary resource to achieve the so-called magic required for universal quantum computation.

“Before these results, we didn’t necessarily know what resources were needed for a physical device to achieve the advantage of quantum information. Now we know one,” said Mark Howard, a postdoctoral fellow at IQC and the lead author of the paper. “As researchers work to build a universal quantum computer, understanding the minimum physical resources required is an important step to finding ways to harness the power of the quantum world.”
Quantum devices are extremely difficult to build because they must operate in an environment that is noise-resistant. The term magic refers to a particular approach to building noise-resistant quantum computers known as magic-state distillation. So-called magic states act as a crucial, but difficult to achieve and maintain, extra ingredient that boosts the power of a quantum device to achieve the improved processing power of a universal quantum computer.
By identifying these magic states as contextual, researchers will be able to clarify the trade-offs involved in different approaches to building quantum devices. The results of the study may also help design new algorithms that exploit the special properties of these magic states more fully.
“These new results give us a deeper understanding of the nature of quantum computation. They also clarify the practical requirements for designing a realistic quantum computer,” said Joseph Emerson, professor of Applied Mathematics and Canadian Institute for Advanced Research fellow. “I expect the results will help both theorists and experimentalists find more efficient methods to overcome the limitations imposed by unavoidable sources of noise and other errors.”
Contextuality was first recognized as a feature of quantum theory almost 50 years ago. The theory showed that it was impossible to explain measurements on quantum systems in the same way as classical systems.
In the classical world, measurements simply reveal properties that the system had, such as colour, prior to the measurement. In the quantum world, the property that you discover through measurement is not the property that the system actually had prior to the measurement process. What you observe necessarily depends on how you carried out the observation.
Imagine turning over a playing card. It will be either a red suit or a black suit - a two-outcome measurement. Now imagine nine playing cards laid out in a grid with three rows and three columns. Quantum mechanics predicts something that seems contradictory – there must be an even number of red cards in every row and an odd number of red cards in every column. Try to draw a grid that obeys these rules and you will find it impossible. It's because quantum measurements cannot be interpreted as merely revealing a pre-existing property in the same way that flipping a card reveals a red or black suit.
Measurement outcomes depend on all the other measurements that are performed – the full context of the experiment.
Contextuality means that quantum measurements can not be thought of as simply revealing some pre-existing properties of the system under study. That's part of the weirdness of quantum mechanics.
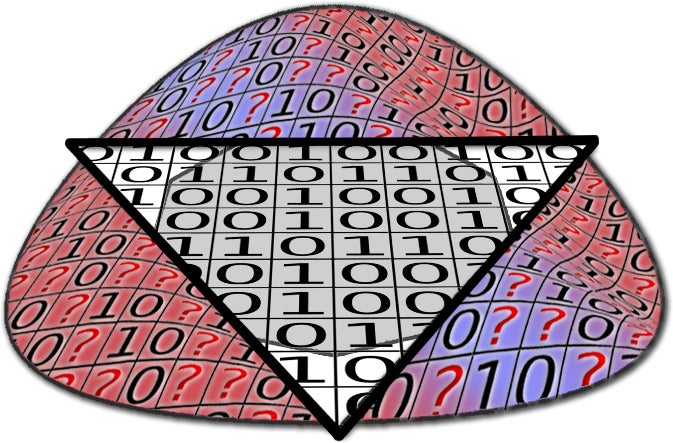
This geometric figure illustrates the concept of magic states and their relation to contextuality. The triangular region contains quantum states that are not magic and do not exhibit contextuality. States outside the triangle do exhibit contextuality and may be useful as a resource in the magic-state model of quantum computing.
About the University of Waterloo
In just half a century, the University of Waterloo, located at the heart of Canada's technology hub, has become one of Canada's leading comprehensive universities with 35,000 full- and part-time students in undergraduate and graduate programs. Waterloo, as home to the world's largest post-secondary co-operative education program, embraces its connections to the world and encourages enterprising partnerships in learning, research and discovery. In the next decade, the university is committed to building a better future for Canada and the world by championing innovation and collaboration to create solutions relevant to the needs of today and tomorrow. For more information about Waterloo, please visit www.uwaterloo.ca.
-30-
Media Contact
Nick Manning
University of Waterloo
519-888-4451
226-929-7627
www.uwaterloo.ca/news
@uWaterlooNews
Attention broadcasters: Waterloo has facilities to provide broadcast quality audio and video feeds with a double-ender studio. Please contact us to book.