Rafael Oliveira joined the Cheriton School of Computer Science in January 2020 as an assistant professor.
He received his PhD in computer science from Princeton University in 2017. After his doctoral degree, he was a postdoctoral researcher at the University of Toronto from 2017 to 2018, then a research fellow at UC Berkeley’s Simons Institute for the Theory of Computing.
Rafael’s research interests lie in the interplay between mathematics and computer science, particularly in how optimization and computational complexity interact with other areas of mathematics and science, such as algebra, invariant theory, quantum information theory and analysis. He uses these connections between optimization, complexity and invariant theory to provide novel algorithms for various computational problems arising in computer science.

Tell us a bit about yourself.
I did my PhD in computer science at Princeton. I was in the theory group and advised by Zeev Dvir, who works on algebraic complexity, coding theory and discrete geometry, which is at the intersection of algebraic geometry and combinatorics. Zeev was my advisor throughout my PhD, but halfway through my doctorate I also started working with Avi Wigderson, who became an informal mentor.
After my PhD, I completed a postdoc position at the University of Toronto and after that I was a research fellow at the Simons Institute for the Theory of Computing at UC Berkeley. The Simons Institute is a fairly recent institute and it was set up to conduct collaborative research in theoretical computer science and related fields.
When did you become interested in computer science?
I grew up in Brazil and as a kid I didn’t have a computer. It was only after I came to the US for my undergrad degree that I began to use computers. But I didn’t start college in computer science. I came to MIT as an undergrad to do math. I liked math a lot. In fact, ever since I was a little kid I’ve loved doing math.
After a while I felt that the math was getting too abstract and I was beginning to lose motivation, and I was thinking why am I studying this? My undergrad advisor at the time said to me, ‘MIT is a big place; go explore it’ so I did. I saw found some theoretical computer science classes and I entered them. It was beautiful because these classes blended something I loved — math — with something that motivated me.
In computer science, you’re given a problem that’s generally simple to understand — such as sorting a list — but to solve that in an optimal way, and to prove that you have the best solution, you need math. I could easily see why you would want to do the task and that’s what got me hooked on computer science. I did a double major — math and computer science — at MIT. I stayed a year afterward at MIT to do my master’s degree to see if I wanted to continue in computer science and to prepare myself for doctoral studies. After that, I started my PhD at Princeton.
What attracted you to the Cheriton School of Computer Science?
A couple of things attracted me to the Cheriton School in particular and the University of Waterloo generally. For a person like me who does theoretical work this is a wonderful place because we have this confluence in the Faculty of Mathematics of combinatorics and optimization on the math side and algorithms and complexity on the computer science side.
Also, the School of Computer Science is known to be very friendly toward theoretical research and mathematical research in computer science. It’s also a strong school academically and the Faculty of Mathematics and the School of Computer Science are filled with amazing people who are excited about theoretical research. I applied selectively for faculty positions and the Cheriton School of Computer Science was among my top choices because it’s one of the top places in the world to do research.
On top of that, because teaching is the other half of a professor’s life, I was attracted to Waterloo because its students are known to be very bright and motivated. This weighed heavily in my decision to apply here. I’m going to be teaching about half of my time and it’s exciting to teach and work with bright students.
As a professor, you meander between research and teaching. The more you teach the better you understand your discipline and the better you understand your discipline the better your research. For me, this interplay is fundamental and that’s why being a prof here is such a huge plus.
Tell us a bit about your research.
Let me back up a bit first. In computer science, we have a whole array of fundamental, basic tasks that we do. Say I ask you to build a website or to program a video game or I give you a list and ask you to sort it. These tasks are fundamentally mathematical problems. Behind the scenes, you have all this mathematics going on so that it all can happen.
I give you an algorithm and it runs in a certain amount of time. If I’m your boss I might ask if you can make the algorithm run faster. If it runs faster it saves time, so it’s easy to understand why you might want to develop faster algorithms. Asking if you can develop a better algorithm is sometimes meant to be is it even possible to develop a better algorithm. This question is really about the limits of computation. In general sense, this is what I do.
You can model a computer mathematically — the actual physical device — and explore what’s possible for that device to do. Here, mathematics is placing a limit on the physical world — for example, what are the fewest number of operations required to sort a list. Let’s say you want to multiple two matrices. This is a fundamental task that’s performed in many scientific disciplines and the problem is algebraic in nature. How fast can you multiple two matrices?
You can use all sorts of algorithms to do that. But if you asked someone to do this, what would the person do? They would do algebraic operations. They would multiple the entries and then sum them. A large field developed to solve these kinds of problems that are algebraic in nature.
How fast can a computer solve an algebraic problem using only algebraic tools — for example, multiplying matrices or decomposing matrices or tensors and higher algebraic objects into simple things. These tasks have connections to many things, machine learning, for example, as well as many other areas. Understanding the complexity — how fast can an algorithm run or the impossibility of having super-fast algorithms for certain problems is what I do.
Let me tell you about one of the main problems in algebraic complexity. In computer science we have this paradigm — given a computational problem, what’s the fastest way a computer can solve it? If I give you a really fast algorithm, it’s considered a good algorithm. And if you prove a lower bound, you have shown that it’s impossible to solve this problem with fewer than a certain number of operations.
The amazing thing about P vs NP — the famous problem in computer science — is that there are all these other problems that are completely understandable, but somehow they capture a lot of other problems. The travelling salesman problem is a good example of this — given a list of cities and the distances between each pair of cities, what’s the shortest possible route that visits each city and returns to the origin city? Somehow, this problem is equivalent to all sorts of other problems, including ones that might surprise you. That’s why the travelling salesman problem is central. The job of complexity theorists is to classify all these problems from easy to hard. And in algebra it’s the same. But how do you model this?
Let’s start with a polynomial. A polynomial is a function. Let’s start with an easy one — the function x,y is the function given by x2 minus y2. Mathematically, it looks like this: f(x,y) = x2–y2
It’s a function you can obtain by performing algebraic operations on the input. Polynomials are fundamentally algebraic objects. If I’m going to multiple two matrices, in the end I’m computing some kind of polynomial. Therefore, you can model all the algebraic computations as essentially computing polynomials. If you solve a P vs NP problem, you solve a lot of other problems that are equivalent to it.
If I’ve managed to convince you that everything algebra is doing is computing some polynomials, the question becomes are there polynomials or families of polynomials that are like the travelling salesman problem? If you can compute them fast, you can compute essentially everything that’s interesting fast.
Classifying this and proving there’s a hard polynomial — that there’s a polynomial that no regular computer can compute — is one of the golden goals. This is called VP vs VNP, the algebraic analogue of P vs NP. Just like in P vs NP, you have the easy polynomials, you have the interesting polynomials and you have everything else — all the polynomials.
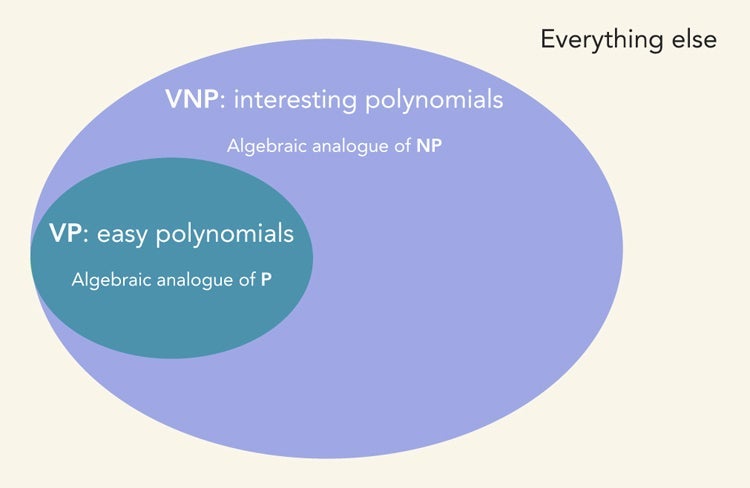
If you look at VP vs VNP, somehow it looks like P is the VP oval and NP is the larger VNP oval. And everything else is the polynomials you can’t hope to compute.
With algebra, it’s the same thing. We have the easy polynomials — VP — and we have the interesting polynomials — VNP — but we don’t know if they’re easy. It’s a huge result that even in algebra we have polynomials that are complete, kind of like the travelling salesman problem of polynomials. Separating these classes is one of the golden goals of what I do and it has applications everywhere. These problems appear in graph theory, they appear in combinatorics, they appear in statistical physics.
So, here’s this thing that’s completely algebraic and it looks like only algebraic things are going on, so how do you do optimization? It turns out there is a correspondence. There’s a correspondence between polynomials and geometric objects. And once you have geometry, you also have a correspondence to optimization.

How does this happen? Say, I give you the parabola y–x2≥ 0. This is the parabola, plus everything on top of it. This is a geometric set.
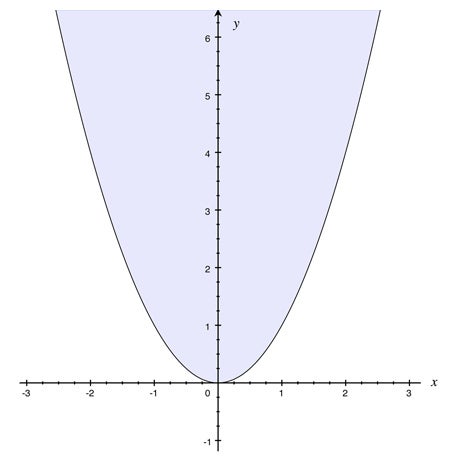
So, algebra somehow has the correspondence to geometry, and geometry has the correspondence to optimization. In many ways, these connections are not well explored. But all of these sets have nice descriptions in algebraic terms. Building this bridge and seeing how they correspond to each other is what I do.
If the geometric nice sets are algebraic, then we can use algebra to understand the nice sets, but we can also use geometry of these nice sets to try to understand algebra. One way to do this is through optimization. I have these nice sets and I can optimize over them and what does the optimum of a particular function tell us about the polynomials in the function. Exploring the interplay between algebra, geometry and optimization is one of the things I do.
Do you see opportunities for new, collaborative research, given the breadth and depth of research conducted at the Cheriton School of Computer Science?
One of the first things I did when I started was to look at what professors here are working on. I wanted to knock on everyone’s door and ask about their research to get an idea about all of the fantastic work being done here, both in applied and theoretical research.
I’d like to learn about everyone’s research for curiosity’s sake, but also to see if their research is something I can contribute to. Even though researchers here have conducted a lot of theoretical work, which is my natural realm of collaboration, I also want to know about the applied research people are working on. This school is very collegial and it can be very fruitful to see what others are doing and to see if there’s a place where you can collaborate.
For example, Lap Chi Lau does research in the optimization realm, so working with him is a natural fit. I also talked with Shalev Ben-David before I joined and we definitely have overlapping areas of interest. I also see a lot of overlap with research that Eric Blais, Mark Giesbrecht and Éric Schost do because they use a lot of algebra in their work. Mark and I have already talked about co-supervising some students.
What do you consider your most significant contribution or work to date?
That would be a series of recent papers that bridge the gap between algebraic geometry and invariant theory in optimization. This work is about the development of fast algorithms for certain optimizations problems that come from algebra, which is this invariant theory.
Who has inspired you most in your academic life?
Like most academics, many people have inspired me throughout my academic life from my early days as an undergraduate. But Avi Wigderson, at Princeton’s Institute for Advanced Study, has had huge influence on me. He became an informal mentor part way through my PhD. He’s very much a person I look up to and I’ve tried to learn as much as I can from him. I’m here and excited about the things I’m doing because of Avi. So, yes, lots of people — professors and fellow students — have inspired me, but Avi in particular has had a profound influence on me.
What do you do in your spare time?
I’m from Brazil, so dancing is a requirement. They kick you out of the country if you don’t dance. [laughs] But I really do love dancing. I haven’t danced that much over the past two years, but when I was in grad school and during my undergraduate degree at MIT a danced a lot — everything from modern dance to ballroom to Latin American dance.
I also got into rock climbing with some friends. And I love sand volleyball and soccer. Playing soccer is mandatory for a Brazilian. It’s a shame soccer isn’t more popular in Canada. I guess it’s the ice and snow that held it back. [laughs]