“From my readings, I have stumbled upon your great website, which is … helping me understand the nature of polyhedra. I have a question regarding the structures you have posted on your site. I am not a mathematician; I am a biologist and therefore my question might sound downright naïve. The structure in question is the near-miss Johnson solid …”
With that email from a biologist in Japan, Cheriton School of Computer Science Professor Craig Kaplan’s curiosity had been piqued. He came to be a collaborator on a research project spanning five countries on three continents that brought together his expertise in geometry and computer graphics with the insights of a team of biochemists, physicists and structural biologists to elucidate the paradoxical geometry of a manufactured protein cage.

Professor Craig Kaplan, a computer scientist with expertise in geometry and computer graphics, holds the hendecagonal near-miss Johnson solid he created out of paper and tape.
The findings of their multidisciplinary study were published recently in Nature, among the most prestigious of scientific journals, in a paper titled “An ultra-stable gold-coordinated protein cage displaying reversible assembly.”
To understand why this molecular cage has paradoxical geometry, it helps to first explore the properties of polyhedra — solid three-dimensional shapes with flat polygonal faces, straight edges and sharp vertices.
The best-known polyhedra, those composed solely of identical regular polygonal faces, are the five Platonic solids — the tetrahedron, cube, octahedron, dodecahedron and icosahedron — shapes that have been known since antiquity. Also well known among mathematicians are the 13 Archimedean solids, along with the prisms and antiprisms. By relaxing the constraints on complete regularity, in 1966 mathematician Norman Johnson enumerated 92 convex polyhedra — the so-called Johnson solids — which have the property that all faces are regular polygons. The list was later proved complete by Victor Zalgaller in 1969.
Many Johnson solids look odd, as though they have been constructed by a child using leftover polygons from other polyhedra. But as strange as they may appear, each one is mathematically perfect. In all 92 Johnson solids, the regular polygons fit together to create a three-dimensional shape without gaps, holes or curves.
“One of the topics I worked on during my PhD was Islamic geometric patterns,” Professor Kaplan explains. “I developed a system for drawing them that depended on constructing tessellations with lots of regular polygons in them. That work led to a paper with George Hart, a famous mathematical and polyhedron sculptor, in which we defined a series of shapes that have regular polygons.”
In the paper, they also discussed solids that were tantalizingly close to being perfect but had in some way missed the mark.
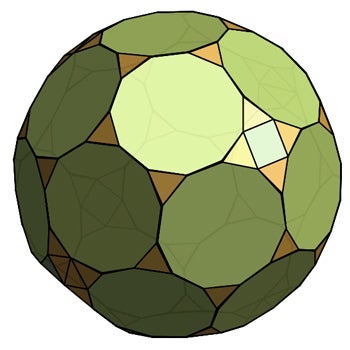
“In some of the solids the left-over spaces were really close to being regular polygons,” Professor Kaplan said. “Maybe the space is so close that you could construct the polyhedron, say by cutting out paper shapes and taping them together, that you’d never notice it would not close up perfectly. We called these shapes near misses. I didn’t have much more to say about the mathematics of near misses, but I put a few of them on my website.”
Near misses are geometric oddballs, as though they are trying really hard to be on Johnson’s list but they fall short in some way. But it turns out that almost being a Johnson solid was the clue that helped explain the structure of a three-dimensional protein molecule manufactured by a research team halfway across the globe.
“I was emailed out of the blue by a researcher in Japan, a member of a team of international researchers, who had constructed a molecular protein cage that had a geometry that shouldn’t work,” Professor Kaplan recounts. “They were trying to understand what it could possibly be. They discovered my near-miss shape online, maybe by searching for polyhedra with 11-sided faces.”
The team, led by Jonathan Heddle from the Małopolska Centre of Biotechnology at Jagiellonian University in Poland, was studying a custom-engineered protein called TRAP — short for trp RNA-binding attenuation protein — which can form an 11-sided ring structure. Using cryo-electron microscopy they saw that under certain conditions in the presence of nanoparticles made of gold, a set of TRAP rings would assemble into a round solid, which they called a TRAP-cage. But the structure of the cage was a mystery because the team didn’t know of a geometric form made from pieces with 11-fold symmetry.
In a sense, Professor Kaplan had already shown that while such a molecule was in the strictest sense mathematically impossible, it might exist in the real world.

“Long before I was contacted, I made a paper model of that shape,” he explained. “I cut out perfect hendecagons — 11-sided polygons — along with equilateral triangles and squares, then taped them together knowing all the while that a closed-up shape shouldn’t be possible, but it’s close enough to being possible that it’ll work.”
The shape can be built because paper can warp a tiny bit, the gaps aren’t perfect, the taping isn’t perfect, Professor Kaplan said, adding that while those imperfections mean the shape is mathematically impossible, in the real world the imperfections balance out and are hard to spot through casual observation.
If we extrapolate from the paper model to the protein cage — the manufactured structure known as a TRAP-cage — could it be that its molecular bonds are giving a bit, too, making it structurally possible?
“It looked like the TRAP rings in their cage were arranged like the hendecagons in my near miss,” Professor Kaplan said. “That’s the amazing thing. If you scale this shape down to molecular size, the order of magnitude of the error is small enough that it falls within the general uncertainty of atomic bond distances.”
The TRAP-cage is a bit more flexible than the near miss made of paper and tape. First, it’s constructed purely from TRAP rings, so you don’t have to worry about fitting squares and triangles into the molecule as you would in the paper model. Second, the rings aren’t actually attached to each other as they would be in a polyhedron; instead, the ring has 11 molecular arms, and the arms from neighbouring rings bond with gold atoms to hold the structure together. This extra flexibility means that you can construct a model cage with even lower error than the original near miss.
Professor Kaplan tested this hypothesis using numerical optimization, searching for a symmetric arrangement of TRAP rings for which the gold bonds would have the correct lengths predicted by chemistry. The goal of the optimization was to minimize the worst error in bond length, while trying to keep the arrangement of TRAP rings as round as possible.
This optimization found virtual cages where the bond lengths between neighbouring rings never deviated by more than one part in a billion from their ideal lengths. For a near miss, it was astonishingly close to a perfect hit.
“Our understanding of physics and chemistry is informed by the uncertainty principle, the recognition that atoms are not solid balls connected by rigid rods,” Professor Kaplan said. “Rather, atoms are better viewed as probability distributions. The fact that atoms are very slightly away from the idealized bond length, presumably just imparts the entire molecule with a little bit extra potential energy, but not enough to break it apart.”
In other words, the TRAP-cage should hold together. It’s a real-world near miss at molecular scale — one you could build out of microscopic pieces without noticing the discrepancy.
“This research project has been a hugely satisfying effort and I’m extremely grateful to have been a part of it,” Professor Kaplan said. “The most satisfying moments of doing research, especially in the interdisciplinary world where I try to work, is ramming two seemingly disconnected ideas together and having these really interesting bits fly out that turn into something wonderful.”
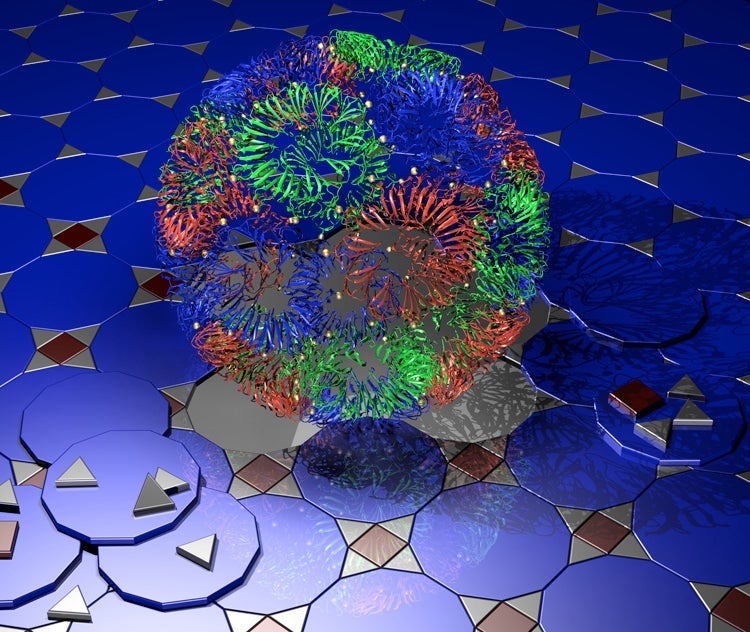
A visualization of the molecular structure of the TRAP-cage, with gold atoms highlighted, sits on a field of two different Euclidean tilings, suggestive of the structure of the original near miss.